On the Flavor Problem in Strongly Coupled Theories - THEP Mainz

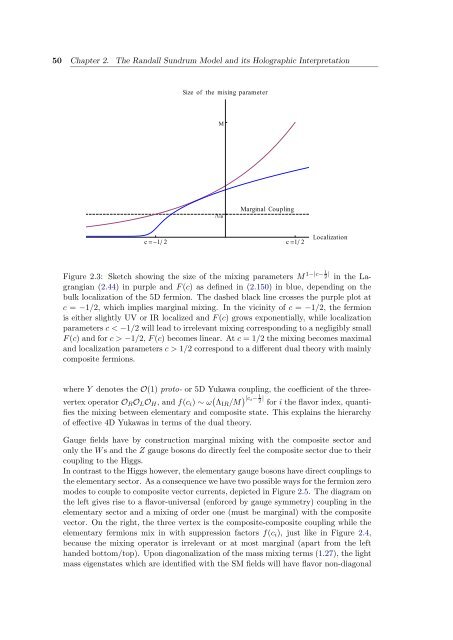
50 Chapter 2. The Randall Sundrum Model and its Holographic Interpretation
Size of the mixing parameter
M
�IR
Marginal Coupling
c ��1� 2 c �1� 2
Localization
1
1−|c− Figure 2.3: Sketch showing the size of the mixing parameters M 2 | in the Lagrangian
(2.44) in purple and F (c) as defined in (2.150) in blue, depending on the
bulk localization of the 5D fermion. The dashed black line crosses the purple plot at
c = −1/2, which implies marginal mixing. In the vicinity of c = −1/2, the fermion
is either slightly UV or IR localized and F (c) grows exponentially, while localization
parameters c < −1/2 will lead to irrelevant mixing corresponding to a negligibly small
F (c) and for c > −1/2, F (c) becomes linear. At c = 1/2 the mixing becomes maximal
and localization parameters c > 1/2 correspond to a different dual theory with mainly
composite fermions.
where Y denotes the O(1) proto- or 5D Yukawa coupling, the coefficient of the threevertex
operator OROLOH, and f(ci) ∼ ω � ΛIR/M � |ci− 1
2 | for i the flavor index, quantifies
the mixing between elementary and composite state. This explains the hierarchy
of effective 4D Yukawas in terms of the dual theory.
Gauge fields have by construction marginal mixing with the composite sector and
only the W s and the Z gauge bosons do directly feel the composite sector due to their
coupling to the Higgs.
In contrast to the Higgs however, the elementary gauge bosons have direct couplings to
the elementary sector. As a consequence we have two possible ways for the fermion zero
modes to couple to composite vector currents, depicted in Figure 2.5. The diagram on
the left gives rise to a flavor-universal (enforced by gauge symmetry) coupling in the
elementary sector and a mixing of order one (must be marginal) with the composite
vector. On the right, the three vertex is the composite-composite coupling while the
elementary fermions mix in with suppression factors f(ci), just like in Figure 2.4,
because the mixing operator is irrelevant or at most marginal (apart from the left
handed bottom/top). Upon diagonalization of the mass mixing terms (1.27), the light
mass eigenstates which are identified with the SM fields will have flavor non-diagonal