LCLS Conceptual Design Report - Stanford Synchrotron Radiation ...

More documents

Recommendations

Info

L C L S C O N C E P T U A L D E S I G N R E P O R T the incoming BC2 bunch length at 195 µm rms. The bunch length after BC2 is adjustable using the R56 of BC2 and the rf phase of L2. The parameters of the BC2 chicane are listed in Table 7.14. Table 7.14 Parameters of 2nd bunch compressor chicane, BC2. Parameter Symbol Unit Value Beam energy E GeV 4.54 Initial rms bunch length σzi µm 195 Final rms bunch length σzf µm 22 RMS incoming relative energy spread (at 4.54 GeV) σδ % 0.76 RMS uncorrelated relative energy spread (at 4.54 GeV, with wiggler) σδ u 10 –5 3 Net momentum compaction R 56 mm −22.5 Net second order momentum compaction T 566 mm +33.8 Total system length (1 st bend to last) Ltotal m 22.1 Floor length of each of four dipole magnets L B m 0.400 Floor length of drift between first two and last two dipoles ∆L m 10 Floor length of drift between center two dipoles ∆Lc m 0.50 Bend angle for each of four dipoles |θ B| deg 1.878 Magnetic field for each of four dipoles |B| kG 12.41 Maximum dispersion in chicane center (≈ beamline excursion) |η max| m 0.341 Slice emittance dilution due to ISR of chicane only (at γε 0 = 1 µm) ∆ε ISR/ε 0 % 0.3 Projected emittance dilution due to CSR (includes all particles) ε x/ε x0 ⎯ 2.5 rms ISR relative energy spread of chicane only (at 4.54 GeV) σ δ ISR 10–6 8.4 rms CSR relative energy spread (at 4.54 GeV) σ δ CSR % 0.053 CSR relative energy loss (at 4.54 GeV) 〈δ CSR〉 % 0.071 A nominal rms final bunch length of 22 µm is used throughout the following descriptions (unless otherwise noted). As in the case of BC1, the center two dipoles will be placed on remotely movable horizontal stages in order to: 1) allow non-LCLS linac operation, 2) to ease dipole field quality tolerances, and 3) to allow a high-resolution BPM to be placed at the center of the chicane. With the dipoles switched off, the BC2 (and the BC1) chicane can then be straightened out. The maximum horizontal beamline excursion at chicane center is equal to the maximum dispersion, |ηmax|, listed in the table. The excursion is toward the tunnel ‘wall’ (north) to keep the ‘aisle’ clear. Figure 7.26 shows the dispersion and beta functions through the BC2 chicane. Magnet locations are shown at the top of the figure. This plot, and other calculations, is made for a net R56 of −22.5 mm. 7-46 ♦ A C C E L E R A T O R
β (m) 120 100 80 60 40 20 0 Q24701 WIGGLER L C L S C O N C E P T U A L D E S I G N R E P O R T QM21 B21 CQ21 B22 β x β y η x 400 405 410 S (m) 415 420 Figure 7.26 Dispersion and beta functions through BC2 chicane for R 56 ≈ −22.5 mm. The energy spread profile monitor is indicated by a small circle at the center of the chicane in schematic at top. The two quadrupoles inside the chicane are for dispersion correction and are nominally switched off. The superconducting wiggler is located at S ≈ 397 m. 7.4.2.2 Momentum Compaction The momentum compaction (R56) for a chicane is given by Eq. (7.12). The second order momentum compaction is T566 ≈ –3R56/2 (as in BC1). A beam delay as described in Eq. (7.13) is also necessary for the L3 rf phase. The L3 rf phase needs to be delayed, with respect to the chicane-off phase, by dφ/dR56 ≈ π/λ ≈ 1.72°/mm (or 38.7° with the nominal BC2 R56 value of −22.5 mm). 7.4.2.3 Incoherent Synchrotron Radiation (ISR) Horizontal emittance dilution will occur if significant energy spread is generated anywhere within the chicane (or the wiggler). Synchrotron radiation within the dipoles generates energy spread, which breaks the linear achromaticity of the chicane and therefore dilutes the horizontal emittance. Using a typical symmetric beta function through a single chicane with its maximum, βmax, at start and end of the chicane and its minimum, βmin, in the middle, and using symbols defined in Table 7.14, then max min B23 CQ22 B24 QM22 Q24901 0.35 0.3 0.25 0.2 0.15 0.1 0.05 β = 2β= 4L + 2∆ L+∆L . (7.21) B c The additive ISR emittance dilution [29] can then be approximated, for ∆ε/ε 0
Page 1 and 2:
Linac Coherent Light Source (LCLS)
Page 3 and 4:
L C L S C O N C E P T U A L D E S I
Page 5 and 6:
Page 7 and 8:
Preface This Conceptual Design Repo
Page 9 and 10:
Page 11 and 12:
Table of Contents 1 Executive Summa
Page 13 and 14:
Page 15 and 16:
Page 17 and 18:
Page 19 and 20:
Page 21 and 22:
Page 23 and 24:
Page 25:
Page 28 and 29:
6. Two experiment halls L C L S C O
Page 30 and 31:
Page 32 and 33:
Page 34 and 35:
Page 36 and 37:
Page 38 and 39:
2.7.1.7 Conventional Facilities L C
Page 40 and 41:
Page 42 and 43:
Page 44 and 45:
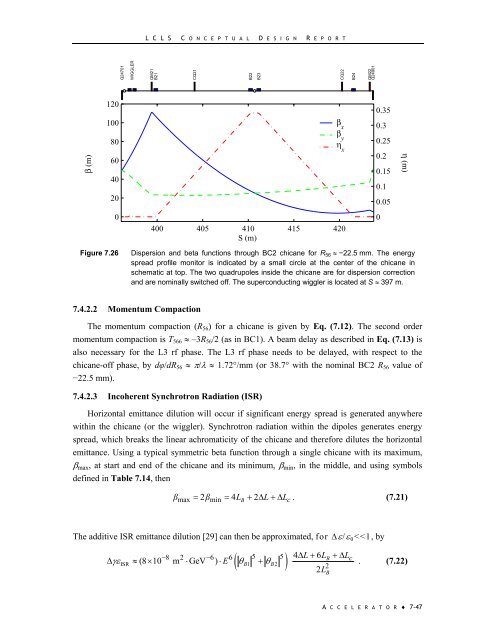
Page 46 and 47:
Page 49 and 50:
3 TECHNICAL SYNOPSIS Scientific Bas
Page 51 and 52:
Page 53 and 54:
Page 55 and 56:
Page 57:
Page 60 and 61:
Page 62 and 63:
Page 64 and 65:
Page 66 and 67:
Page 68 and 69:
Page 70 and 71:
Page 72 and 73:
Page 74 and 75:
Page 76 and 77:
Page 78 and 79:
Page 80 and 81:
Page 82 and 83:
Page 84 and 85:
Page 86 and 87:
Page 89 and 90:
5 TECHNICAL SYNOPSIS FEL Parameters
Page 91 and 92:
Page 93 and 94:
and the total peak beam power L C L
Page 95 and 96:
Page 97 and 98:
Page 99 and 100:
Page 101 and 102:
Page 103 and 104:
Page 105 and 106:
5.4.2.2 Case II - High Charge Limit
Page 107 and 108:
Page 109 and 110:
Page 111 and 112:
Page 113 and 114:
∆P ∆I sat pl / P / I sat pk L C
Page 115 and 116:
Page 117 and 118:
5.9 Summary L C L S C O N C E P T U
Page 119 and 120:
6 Injector TECHNICAL SYNOPSIS The i
Page 121 and 122:
Page 123 and 124:
Page 125 and 126:
εn,x (µm) 4 3 2 1 4-2001 8560A95
Page 127 and 128:
Page 129 and 130:
Page 131 and 132:
Page 133 and 134:
Page 135 and 136:
Page 137 and 138:
Page 139 and 140:
Quantum Yield (electrons/photon) 10
Page 141 and 142:
Bz (T) 0.3 0.2 0.1 1-2002 8560A92 L
Page 143 and 144:
Page 145 and 146:
Page 147 and 148:
Page 149 and 150:
Page 151 and 152:
Page 153 and 154:
Master Clock 9.917 MHz x8 x6 x6 Df
Page 155 and 156:
Page 157 and 158:
Page 159 and 160:
1-2002 8560A198 Linac Center Line L
Page 161 and 162:
Page 163 and 164:
Page 165 and 166:
B z (kG) 3 2 1 4-2001 8560A91 L C L
Page 167 and 168:
Page 169 and 170:
γε x,y (µm) 3 2 1 0 3-2001 8560A
Page 171 and 172:
γεx,y (µm) yn 10 0 -10 -10 0 10
Page 173 and 174:
σ γ /γ 0 (percent) ∆N/N 0.02 0
Page 175 and 176:
5 0 -5 5 0 -5 5 0 -5 L C L S C O N
Page 177 and 178:
Table 6.5 PARMELA Output Parameters
Page 179 and 180:
gama x (micro.m) 3 2 1 0 0 L C L S
Page 181 and 182: ∆E/E 0 (%) ∆N/N 0 -1 -2 0.02 0
Page 183 and 184: L C L S C O N C E P T U A L D E S I
Page 185: L C L S C O N C E P T U A L D E S I
Page 204 and 205: 〈∆E/E 0 〉 /% I pk /I pk0 0.1
Page 216 and 217: β (m) 35 30 25 20 15 10 5 0 K21_1B
Page 220 and 221: β (m) 60 50 40 30 20 10 0 L C L S
Page 256 and 257: economic reasons. L C L S C O N C E
Page 268 and 269: Phase [deg. S-band] L C L S C O N C
Page 272 and 273: New Solid-State Sub-Booster and Ele
Page 278 and 279: 7.8.2 Bunch Length Diagnostics L C
Page 282 and 283:
Page 284 and 285:
Page 286 and 287:
Page 288 and 289:
Page 290 and 291:
Page 292 and 293:
Page 294 and 295:
Page 296 and 297:
Magnet String Location Existing, Ne
Page 298 and 299:
Page 300 and 301:
Page 302 and 303:
Page 304 and 305:
8.1 Overview 8.1.1 Introduction L C
Page 306 and 307:
Page 308 and 309:
Page 310 and 311:
Page 312 and 313:
Page 314 and 315:
Page 316 and 317:
Page 318 and 319:
Page 320 and 321:
Page 322 and 323:
Page 324 and 325:
Page 326 and 327:
Mu in the pole, for mu
Page 328 and 329:
Page 330 and 331:
Page 332 and 333:
Page 334 and 335:
Page 336 and 337:
Page 338 and 339:
Page 340 and 341:
Page 342 and 343:
Page 344 and 345:
Page 346 and 347:
Page 348 and 349:
Page 350 and 351:
Page 352 and 353:
Page 354 and 355:
Gasload (Torr-l/sec-cm) (x10 -12 )
Page 356 and 357:
Page 358 and 359:
Page 360 and 361:
Page 362 and 363:
Page 364 and 365:
Page 366 and 367:
Page 368 and 369:
8.10.4 Conclusion L C L S C O N C E
Page 370 and 371:
Page 372 and 373:
Page 374 and 375:
Page 376 and 377:
x θ j > 0 L C L S C O N C E P T U
Page 378 and 379:
Page 380 and 381:
Page 382 and 383:
Page 384 and 385:
Page 386 and 387:
Quad ∆X/µm Quad ∆Y/µm −500
Page 388 and 389:
∆X/µm ∆Y/µm L C L S C O N C E
Page 390 and 391:
Page 392 and 393:
8.13.2 Undulator Cell Structure L C
Page 394 and 395:
Page 396 and 397:
Page 398 and 399:
Page 400 and 401:
Page 402 and 403:
Page 404 and 405:
Page 406 and 407:
Page 408 and 409:
9.2 Layout and Optics 9.2.1 Experim
Page 410 and 411:
Fast Valve L C L S C O N C E P T U
Page 412 and 413:
Page 414 and 415:
0.01 10 -4 10 -6 10 -8 10 -10 10 -1
Page 416 and 417:
Page 418 and 419:
Table 9.5 Mirror requirements L C L
Page 420 and 421:
Refractive Focusing System L C L S
Page 422 and 423:
Page 424 and 425:
Pulse Split/Delay L C L S C O N C E
Page 426 and 427:
Page 428 and 429:
Page 430 and 431:
Figure 9.20 LCLS Ion Chamber L C L
Page 432 and 433:
Page 434 and 435:
9.4.3.2 Pulse Length L C L S C O N
Page 436 and 437:
9.4.3.6 Divergence L C L S C O N C
Page 438 and 439:
10 Conventional Facilities TECHNICA
Page 440 and 441:
1-2002 8560A198 Linac Center Line L
Page 442 and 443:
Page 444 and 445:
Figure 10.6 Near hall floor plan 10
Page 446 and 447:
Page 449 and 450:
11 Controls TECHNICAL SYNOPSIS The
Page 451 and 452:
Page 453 and 454:
Page 455 and 456:
11.5.3 Motion Controls L C L S C O
Page 457 and 458:
Page 459:
Page 462 and 463:
12.1 Procedural Overview L C L S C
Page 464 and 465:
Page 466 and 467:
Page 468 and 469:
Page 470 and 471:
Page 472 and 473:
Page 474 and 475:
Page 476 and 477:
Page 478 and 479:
Page 481 and 482:
13 Environment, Safety and Health a
Page 483 and 484:
Table 13-1 Hazard Identification an
Page 485 and 486:
13.1 Ionizing Radiation The design
Page 487 and 488:
Table 13-2 Minimum Training Require
Page 489 and 490:
Page 491 and 492:
Page 493 and 494:
Page 495:
13.10 SLAC References L C L S C O N
Page 498 and 499:
L C L S D E S I G N S T U D Y R E P
Page 500 and 501:
Page 502 and 503:
Page 504 and 505:
Page 506 and 507:
Page 508 and 509:
Page 510 and 511:
Page 512 and 513:
Page 515 and 516:
15 TECHNICAL SYNOPSIS Work Breakdow
Page 517 and 518:
Page 519 and 520:
A A.1 FEL-Physics A.1.1 Performance
Page 521 and 522:
A.2 Photo-Injector A.2.1 Gun-Laser
Page 523 and 524:
A.2.3.2 Electron Beam L C L S C O N
Page 525 and 526:
A.2.4.7 Vacuum L C L S C O N C E P
Page 527 and 528:
Page 529 and 530:
Page 531 and 532:
Page 533 and 534:
A.3.8 DL-2 A.3.8.1 Subsystem L C L
Page 535 and 536:
A.4 Undulator A.4.1 Undulator A.4.1
Page 537 and 538:
Page 539 and 540:
Page 541 and 542:
Page 543 and 544:
B Control Points B.1 Injector Contr
Page 545 and 546:
Page 547 and 548:
C Glossary ACO Anneaux Collisions O
Page 549 and 550:
Page 551 and 552:
Page 553:
show all

LCLS Conceptual Design Report - Stanford Synchrotron Radiation ...

Create successful ePaper yourself

Delete template?

Save as template?