The mechanical effects of short-circuit currents in - Montefiore

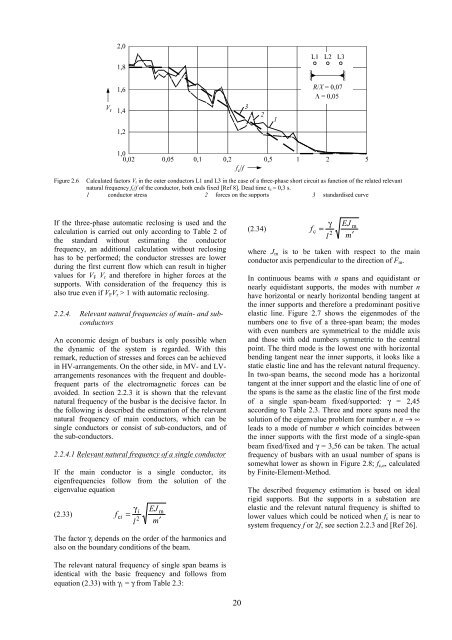
Figure 2.6 Calculated factors Vr in the outer conductors L1 and L3 in the case of a three-phase short circuit as function of the related relevant
natural frequency fc/f of the conductor, both ends fixed [Ref 8]. Dead time tu = 0,3 s.
1 conductor stress 2 forces on the supports 3 standardised curve
If the three-phase automatic reclosing is used and the
calculation is carried out only according to Table 2 of
the standard without estimating the conductor
frequency, an additional calculation without reclosing
has to be performed; the conductor stresses are lower
during the first current flow which can result in higher
values for VF Vr and therefore in higher forces at the
supports. With consideration of the frequency this is
also true even if VFVr > 1 with automatic reclosing.
2.2.4. Relevant natural frequencies of main- and subconductors
An economic design of busbars is only possible when
the dynamic of the system is regarded. With this
remark, reduction of stresses and forces can be achieved
in HV-arrangements. On the other side, in MV- and LVarrangements
resonances with the frequent and doublefrequent
parts of the electromagnetic forces can be
avoided. In section 2.2.3 it is shown that the relevant
natural frequency of the busbar is the decisive factor. In
the following is described the estimation of the relevant
natural frequency of main conductors, which can be
single conductors or consist of sub-conductors, and of
the sub-conductors.
2.2.4.1 Relevant natural frequency of a single conductor
If the main conductor is a single conductor, its
eigenfrequencies follow from the solution of the
eigenvalue equation
(2.33)
f
c i
γ
=
l
i
2
EJ
m′
The factor γi depends on the order of the harmonics and
also on the boundary conditions of the beam.
The relevant natural frequency of single span beams is
identical with the basic frequency and follows from
equation (2.33) with γ1 = γ from Table 2.3:
m
20
(2.34)
f
c
γ
=
2
l
EJ
m′
where Jm is to be taken with respect to the main
conductor axis perpendicular to the direction of Fm.
In continuous beams with n spans and equidistant or
nearly equidistant supports, the modes with number n
have horizontal or nearly horizontal bending tangent at
the inner supports and therefore a predominant positive
elastic line. Figure 2.7 shows the eigenmodes of the
numbers one to five of a three-span beam; the modes
with even numbers are symmetrical to the middle axis
and those with odd numbers symmetric to the central
point. The third mode is the lowest one with horizontal
bending tangent near the inner supports, it looks like a
static elastic line and has the relevant natural frequency.
In two-span beams, the second mode has a horizontal
tangent at the inner support and the elastic line of one of
the spans is the same as the elastic line of the first mode
of a single span-beam fixed/supported: γ = 2,45
according to Table 2.3. Three and more spans need the
solution of the eigenvalue problem for number n. n → ∞
leads to a mode of number n which coincides between
the inner supports with the first mode of a single-span
beam fixed/fixed and γ = 3,56 can be taken. The actual
frequency of busbars with an usual number of spans is
somewhat lower as shown in Figure 2.8; fc,n, calculated
by Finite-Element-Method.
The described frequency estimation is based on ideal
rigid supports. But the supports in a substation are
elastic and the relevant natural frequency is shifted to
lower values which could be noticed when fc is near to
system frequency f or 2f, see section 2.2.3 and [Ref 26].
m