Applied numerical modeling of saturated / unsaturated flow and ...

C. Beyer et al. / Journal of Contaminant Hydrology 87 (2006) 73–95
medians. Only for L4 plume length overestimation is observed and uncertainty is increased in
comparison to case A.
6.3. Case C: estimation of Michaelis–Menten kinetics parameters and plume lengths for plumes
following Michaelis–Menten degradation kinetics
6.3.1. Estimation of rate parameters
As demonstrated in case B, using a first order kinetics approximation for plumes following MM
degradation kinetics introduces an additional error, yielding less conservative estimates of plume
lengths (L1−L3) as well as higher uncertainty (L4). Therefore, method 5 for the estimation of the
MM parameters is tested by application to the contaminant plumes following MM degradation
kinetics (see Table 1). Using the same concentration vs. distance data as in Section 6.2, MM
parameters kmax and MC are estimated by a linear fit as explained in Section 4.1. These parameters
then are used to calculate the length of the contaminant plumes LMM by equation (10) (Table 3).
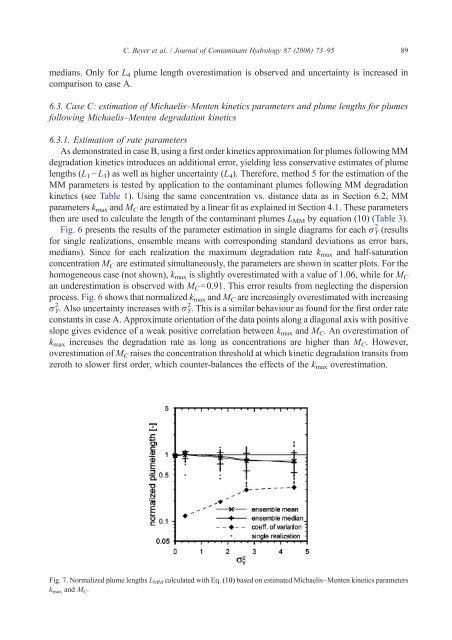
Fig. 6 presents the results of the parameter estimation in single diagrams for each σ Y 2 (results
for single realizations, ensemble means with corresponding standard deviations as error bars,
medians). Since for each realization the maximum degradation rate kmax and half-saturation
concentration MC are estimated simultaneously, the parameters are shown in scatter plots. For the
homogeneous case (not shown), kmax is slightly overestimated with a value of 1.06, while for MC
an underestimation is observed with MC=0.91. This error results from neglecting the dispersion
process. Fig. 6 shows that normalized kmax and MC are increasingly overestimated with increasing
σY 2 . Also uncertainty increases with σY 2 . This is a similar behaviour as found for the first order rate
constants in case A. Approximate orientation of the data points along a diagonal axis with positive
slope gives evidence of a weak positive correlation between k max and M C. An overestimation of
kmax increases the degradation rate as long as concentrations are higher than MC. However,
overestimation of MC raises the concentration threshold at which kinetic degradation transits from
zeroth to slower first order, which counter-balances the effects of the kmax overestimation.
Fig. 7. Normalized plume lengths LMM calculated with Eq. (10) based on estimated Michaelis–Menten kinetics parameters
k max and M C.
89