Méthodes de Monte Carlo appliquées au pricing d ... - Maths-fi.com

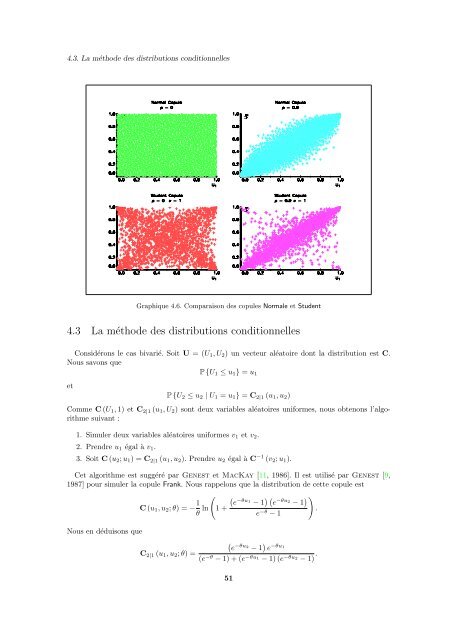
4.3. La méthode des distributions conditionnellesGraphique 4.6. Comparaison des copules Normale et Student4.3 La méthode des distributions conditionnellesConsidérons le cas bivarié. Soit U = (U 1 , U 2 ) un vecteur aléatoire dont la distribution est C.Nous savons queP {U 1 ≤ u 1 } = u 1etP {U 2 ≤ u 2 | U 1 = u 1 } = C 2|1 (u 1 , u 2 )Comme C (U 1 , 1) et C 2|1 (u 1 , U 2 ) sont deux variables aléatoires uniformes, nous obtenons l’algorithmesuivant :1. Simuler deux variables aléatoires uniformes v 1 et v 2 .2. Prendre u 1 égal à v 1 .3. Soit C (u 2 ; u 1 ) = C 2|1 (u 1 , u 2 ). Prendre u 2 égal à C −1 (v 2 ; u 1 ).Cet algorithme est suggéré par Genest et MacKay [11, 1986]. Il est utilisé par Genest [9,1987] pour simuler la copule Frank. Nous rappelons que la distribution de cette copule est(e−θu 1− 1 ) ( e −θu2 − 1 ) )Nous en déduisons queC (u 1 , u 2 ; θ) = − 1 θ ln (1 +C 2|1 (u 1 , u 2 ; θ) =e −θ − 1(e−θu 2− 1 ) e −θu1(e −θ − 1) + (e −θu1 − 1) (e −θu2 − 1) ..51