Segmentation of Stochastic Images using ... - Jacobs University
Segmentation of Stochastic Images using ... - Jacobs University
Segmentation of Stochastic Images using ... - Jacobs University
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
7.5 <strong>Segmentation</strong> <strong>of</strong> <strong>Stochastic</strong> <strong>Images</strong> Using <strong>Stochastic</strong> Level Sets<br />
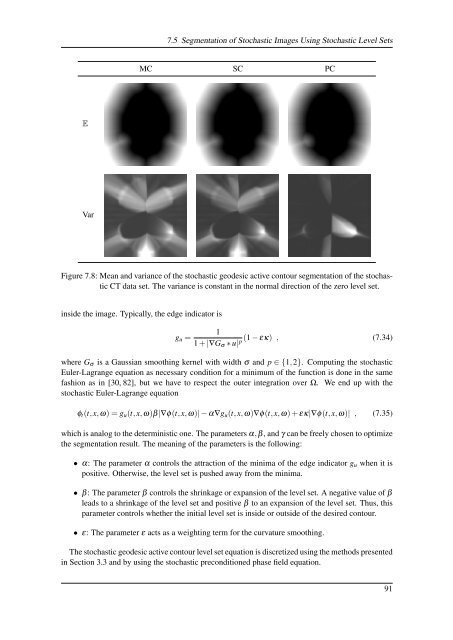
MC SC PC<br />
E<br />
Var<br />
Figure 7.8: Mean and variance <strong>of</strong> the stochastic geodesic active contour segmentation <strong>of</strong> the stochastic<br />
CT data set. The variance is constant in the normal direction <strong>of</strong> the zero level set.<br />
inside the image. Typically, the edge indicator is<br />
g u =<br />
1<br />
(1 − εκ) , (7.34)<br />
1 + |∇G σ ∗ u| p<br />
where G σ is a Gaussian smoothing kernel with width σ and p ∈ {1,2}. Computing the stochastic<br />
Euler-Lagrange equation as necessary condition for a minimum <strong>of</strong> the function is done in the same<br />
fashion as in [30, 82], but we have to respect the outer integration over Ω. We end up with the<br />
stochastic Euler-Lagrange equation<br />
φ t (t,x,ω) = g u (t,x,ω)β|∇φ(t,x,ω)| − α∇g u (t,x,ω)∇φ(t,x,ω) + εκ|∇φ(t,x,ω)| , (7.35)<br />
which is analog to the deterministic one. The parameters α,β, and γ can be freely chosen to optimize<br />
the segmentation result. The meaning <strong>of</strong> the parameters is the following:<br />
• α: The parameter α controls the attraction <strong>of</strong> the minima <strong>of</strong> the edge indicator g u when it is<br />
positive. Otherwise, the level set is pushed away from the minima.<br />
• β: The parameter β controls the shrinkage or expansion <strong>of</strong> the level set. A negative value <strong>of</strong> β<br />
leads to a shrinkage <strong>of</strong> the level set and positive β to an expansion <strong>of</strong> the level set. Thus, this<br />
parameter controls whether the initial level set is inside or outside <strong>of</strong> the desired contour.<br />
• ε: The parameter ε acts as a weighting term for the curvature smoothing.<br />
The stochastic geodesic active contour level set equation is discretized <strong>using</strong> the methods presented<br />
in Section 3.3 and by <strong>using</strong> the stochastic preconditioned phase field equation.<br />
91