Segmentation of Stochastic Images using ... - Jacobs University

Chapter 6 Segmentation of Stochastic Images Using Elliptic SPDEs
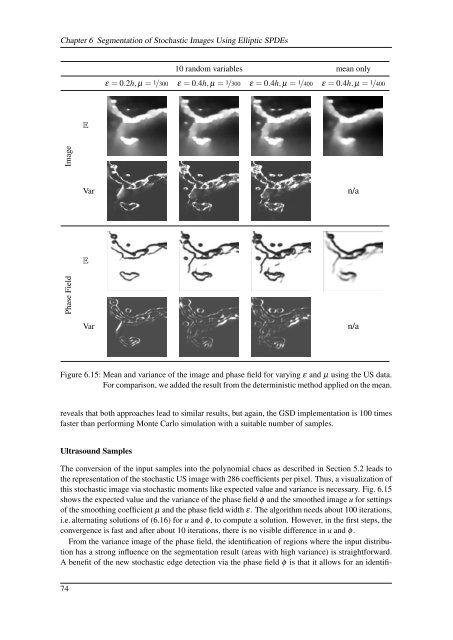
10 random variables mean only
ε = 0.2h, µ = 1/300 ε = 0.4h, µ = 1/300 ε = 0.4h, µ = 1/400 ε = 0.4h, µ = 1/400
E
Image
Var
n/a
E
Phase Field
Var
n/a
Figure 6.15: Mean and variance of the image and phase field for varying ε and µ using the US data.
For comparison, we added the result from the deterministic method applied on the mean.
reveals that both approaches lead to similar results, but again, the GSD implementation is 100 times
faster than performing Monte Carlo simulation with a suitable number of samples.
Ultrasound Samples
The conversion of the input samples into the polynomial chaos as described in Section 5.2 leads to
the representation of the stochastic US image with 286 coefficients per pixel. Thus, a visualization of
this stochastic image via stochastic moments like expected value and variance is necessary. Fig. 6.15
shows the expected value and the variance of the phase field φ and the smoothed image u for settings
of the smoothing coefficient µ and the phase field width ε. The algorithm needs about 100 iterations,
i.e. alternating solutions of (6.16) for u and φ, to compute a solution. However, in the first steps, the
convergence is fast and after about 10 iterations, there is no visible difference in u and φ.
From the variance image of the phase field, the identification of regions where the input distribution
has a strong influence on the segmentation result (areas with high variance) is straightforward.
A benefit of the new stochastic edge detection via the phase field φ is that it allows for an identifi-
74