Segmentation of Stochastic Images using ... - Jacobs University

More documents

Recommendations

Info

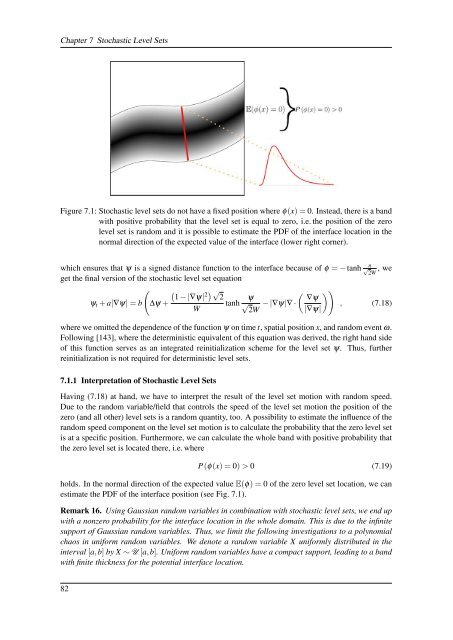
Chapter 7 Stochastic Level Sets Figure 7.1: Stochastic level sets do not have a fixed position where φ(x) = 0. Instead, there is a band with positive probability that the level set is equal to zero, i.e. the position of the zero level set is random and it is possible to estimate the PDF of the interface location in the normal direction of the expected value of the interface (lower right corner). which ensures that ψ is a signed distance function to the interface because of φ = −tanh √ 2W , we get the final version of the stochastic level set equation ( ( 1 − |∇ψ| 2 )√ 2 ψ t + a|∇ψ| = b ∆ψ + tanh ψ ( ) ) ∇ψ √ − |∇ψ|∇ · , (7.18) W 2W |∇ψ| where we omitted the dependence of the function ψ on time t, spatial position x, and random event ω. Following [143], where the deterministic equivalent of this equation was derived, the right hand side of this function serves as an integrated reinitialization scheme for the level set ψ. Thus, further reinitialization is not required for deterministic level sets. 7.1.1 Interpretation of Stochastic Level Sets Having (7.18) at hand, we have to interpret the result of the level set motion with random speed. Due to the random variable/field that controls the speed of the level set motion the position of the zero (and all other) level sets is a random quantity, too. A possibility to estimate the influence of the random speed component on the level set motion is to calculate the probability that the zero level set is at a specific position. Furthermore, we can calculate the whole band with positive probability that the zero level set is located there, i.e. where P(φ(x) = 0) > 0 (7.19) holds. In the normal direction of the expected value E(φ) = 0 of the zero level set location, we can estimate the PDF of the interface position (see Fig. 7.1). Remark 16. Using Gaussian random variables in combination with stochastic level sets, we end up with a nonzero probability for the interface location in the whole domain. This is due to the infinite support of Gaussian random variables. Thus, we limit the following investigations to a polynomial chaos in uniform random variables. We denote a random variable X uniformly distributed in the interval [a,b] by X ∼ U [a,b]. Uniform random variables have a compact support, leading to a band with finite thickness for the potential interface location. n 82
7.2 Discretization of the Stochastic Level Set Equation Stochastic Signed Distance Functions It is desirable to use signed distance functions as level sets in the stochastic context, too. A stochastic signed distance function has to be a classical signed distance function for every realization ω ∈ Ω. Theorem 7.1. A stochastic signed distance function fulfills E(|∇φ|) = 1 and Var(|∇φ|) = 0. Proof. The first property is ensured by the second property by ∫ ∫ E(|∇φ(x)|) = |∇φ(x,ω)|dω = 1 dω = 1 , (7.20) Ω Ω ∫ ∫ Var(|∇φ(x)|) = (|∇φ(x,ω)| − 1) 2 dω = 0 dω = 0 . (7.21) Ω Ω 7.2 Discretization of the Stochastic Level Set Equation For the numerical tests, we discretize (7.18) using the explicit Euler scheme for the discretization of the time derivative. The time discrete version of (7.18) is ( ( √ 2 ψ t+τ = ψ t +τ −a|∇ψ t | + b ∆ψ t + W ( 1 − |∇ψ t | 2) ( ) )) tanh √ ψt ∇ψ − |∇ψ t t |∇ · 2W |∇ψ t , (7.22) | where ψ t is the phase field at time t. The spatial discretization is done via a uniform grid like in Section 5.1. The stochastic part is discretized using the polynomial chaos. Thus, we have to build numerical schemes for the gradient norm, the curvature, and the hyperbolic tangent that deal with polynomial chaos expansions. Gradient Norm and Laplacian The gradient norm is computed using finite difference schemes. The directional derivatives are computed using central differences in the interior of the domain and forward resp. backward differences at the domain boundary. The necessary computations of the square and the square root are performed using the methods from Section 3.3. The Laplacian is computed as the sum of the second directional derivatives, which we compute using central differences in the interior and forward resp. backward differences at the boundary. Hyperbolic Tangent We compute the hyperbolic tangent using tanhx = 1 − 2(exp(2x) + 1) −1 . Thus, we use the computation of the exponential function in the polynomial chaos from Section 3.3 and other methods from there, i.e. we compute the Galerkin projection of the hyperbolic tangent on the polynomial chaos. Curvature The computation of the curvature is the most critical process for the computation of the update, because the update is done in the whole domain, not in a narrow band around the zero level set. This makes it necessary to compute a stable curvature even in regions with a high curvature. These regions arise in simple settings, e.g. when the level set is initialized as a circle. The curvature in the midpoint of the circle goes to infinity. We use a method for the stable curvature computation proposed by Sun 83
Page 1:
Segmentation of Stochastic Images u
Page 5:
Abstract The task of segmentation,
Page 8 and 9:
7.5 Segmentation of Stochastic Imag
Page 11 and 12:
Chapter 1 Introduction The developm
Page 13 and 14:
Figure 1.3: This thesis combines fi
Page 15:
the presentation of the stochastic
Page 18 and 19:
Chapter 2 Image Segmentation and Li
Page 20 and 21:
Page 22 and 23:
Page 24 and 25:
Page 26 and 27:
Page 28 and 29:
Page 30 and 31:
Page 32 and 33:
Page 34 and 35:
Page 36 and 37:
Chapter 3 SPDEs and Polynomial Chao
Page 38 and 39:
Page 40 and 41:
Page 42 and 43: Chapter 3 SPDEs and Polynomial Chao
Page 48 and 49: Chapter 4 Discretization of SPDEs F
Page 50 and 51: Chapter 4 Discretization of SPDEs 4
Page 52 and 53: Chapter 4 Discretization of SPDEs a
Page 58 and 59: Chapter 5 Stochastic Images
Page 60 and 61: Chapter 5 Stochastic Images Figure
Page 62 and 63: Chapter 5 Stochastic Images like qu
Page 64 and 65: Chapter 5 Stochastic Images Figure
Page 67 and 68: Chapter 6 Segmentation of Stochasti
Page 69 and 70: 6.1 Random Walker Segmentation on S
Page 77 and 78: 6.2 Ambrosio-Tortorelli Segmentatio
Page 87: 6.2 Ambrosio-Tortorelli Segmentatio
Page 90 and 91: Chapter 7 Stochastic Level Sets whe
Page 94 and 95: Chapter 7 Stochastic Level Sets and
Page 96 and 97: Chapter 7 Stochastic Level Sets rar
Page 98 and 99: Chapter 7 Stochastic Level Sets Fig
Page 100 and 101: Chapter 7 Stochastic Level Sets MC
Page 106 and 107: Chapter 7 Stochastic Level Sets act
Page 108 and 109: Chapter 8 Segmentation of Classical
Page 118 and 119: Chapter 9 Summary, Discussion, and
Page 121 and 122: List of Figures 1.1 Left: CT image
Page 123 and 124: List of Figures 6.2 Mean and varian
Page 125: List of Figures 7.12 Mean (left) of
Page 129 and 130: Appendix A Publications Written Dur
Page 131 and 132: Bibliography [14] L. Ambrosio and M
Page 133 and 134: Bibliography [46] B. Echebarria, R.
Page 135 and 136: Bibliography [81] B. N. Khoromskij
Page 137 and 138: Bibliography [113] A. Nouy. A gener
Page 139: Bibliography [147] J. Tryoen, O. Le
show all

Segmentation of Stochastic Images using ... - Jacobs University

Create successful ePaper yourself

Delete template?

Save as template?