Segmentation of Stochastic Images using ... - Jacobs University

More documents

Recommendations

Info

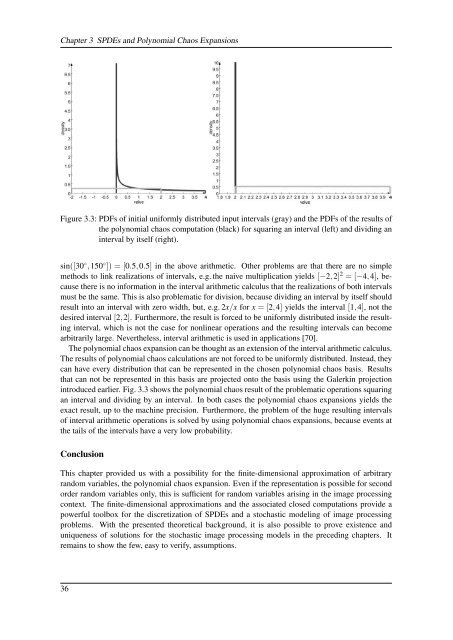
Chapter 3 SPDEs and Polynomial Chaos Expansions Figure 3.3: PDFs of initial uniformly distributed input intervals (gray) and the PDFs of the results of the polynomial chaos computation (black) for squaring an interval (left) and dividing an interval by itself (right). sin([30 ◦ ,150 ◦ ]) = [0.5,0.5] in the above arithmetic. Other problems are that there are no simple methods to link realizations of intervals, e.g. the naive multiplication yields [−2,2] 2 = [−4,4], because there is no information in the interval arithmetic calculus that the realizations of both intervals must be the same. This is also problematic for division, because dividing an interval by itself should result into an interval with zero width, but, e.g. 2x/x for x = [2,4] yields the interval [1,4], not the desired interval [2,2]. Furthermore, the result is forced to be uniformly distributed inside the resulting interval, which is not the case for nonlinear operations and the resulting intervals can become arbitrarily large. Nevertheless, interval arithmetic is used in applications [70]. The polynomial chaos expansion can be thought as an extension of the interval arithmetic calculus. The results of polynomial chaos calculations are not forced to be uniformly distributed. Instead, they can have every distribution that can be represented in the chosen polynomial chaos basis. Results that can not be represented in this basis are projected onto the basis using the Galerkin projection introduced earlier. Fig. 3.3 shows the polynomial chaos result of the problematic operations squaring an interval and dividing by an interval. In both cases the polynomial chaos expansions yields the exact result, up to the machine precision. Furthermore, the problem of the huge resulting intervals of interval arithmetic operations is solved by using polynomial chaos expansions, because events at the tails of the intervals have a very low probability. Conclusion This chapter provided us with a possibility for the finite-dimensional approximation of arbitrary random variables, the polynomial chaos expansion. Even if the representation is possible for second order random variables only, this is sufficient for random variables arising in the image processing context. The finite-dimensional approximations and the associated closed computations provide a powerful toolbox for the discretization of SPDEs and a stochastic modeling of image processing problems. With the presented theoretical background, it is also possible to prove existence and uniqueness of solutions for the stochastic image processing models in the preceding chapters. It remains to show the few, easy to verify, assumptions. 36
Chapter 4 Discretization of SPDEs The discretization of SPDEs is an active research field [47, 159]. Besides the discretization based on sampling approaches like Monte Carlo simulation or stochastic collocation, there are methods for the intrusive computation of stochastic solutions in the literature. Intrusive means that we do not generate the solutions based on sampling strategies and we cannot reuse deterministic algorithms for the solution at the sampling points. This makes it necessary to develop new algorithms, but has the advantage that these algorithms are more efficient than the classical sampling approaches. This thesis focuses on intrusive methods. We present the sampling based approaches as well, but use them to verify the correctness of the intrusive algorithms and implementations only. The intrusive methods presented in this thesis range from the stochastic finite difference method based on polynomial chaos expansions to the generalized spectral decomposition [113–115, 117, 118], a method allowing to speed up the solution process of the stochastic finite element method (SFEM) [54]. 4.1 Sampling Based Discretization of SPDEs Since the mid of the 20 th century [100, 101] authors developed sampling based algorithms for the simulation of stochastic processes, starting with the development of the Monte Carlo method. Later, advanced sampling-based methods like the stochastic collocation method and improvements of these methods e.g. the combination of stochastic collocation and polynomial chaos expansions or the use of sparse grids based on a Smolyak construction [140] have been developed. 4.1.1 Monte Carlo Simulation Monte Carlo simulation is the simplest technique for the discretization of random variables and SPDEs. A set of samples is generated randomly from the known distribution of the random variables via a pseudo random number generator like [97]. We can use the well-known deterministic algorithms on these samples and compute from the results approximations to stochastic quantities like expected value, variance, etc. using well-known formulas. For example, when we computed the solution of R samples, approximate expected value and variance are E(x) ≈ ¯x = 1 R ∑R i=1 x i and Var(x) ≈ 1 R − 1 ∑R i=1 (x i − ¯x) 2 . (4.1) The main drawback of the Monte Carlo method is the slow convergence. In fact, Kendall [79] showed for the Monte Carlo method that the convergence of the samples mean towards the expected value is of order O(σ/ √ R). Despite the slow convergence rate, Monte Carlo methods are widely used (see e.g. [88, 94, 133]) due to the simple implementation and the possibility to reuse deterministic code. 4.1.2 Stochastic Collocation During the last years, a variety of stochastic collocation (SC) techniques was developed. These techniques range from simple collocation techniques over sparse grid techniques to SC techniques allowing to obtain polynomial chaos coefficient (see [159] for a more detailed review). 37
Page 1: Segmentation of Stochastic Images u
Page 5: Abstract The task of segmentation,
Page 8 and 9: 7.5 Segmentation of Stochastic Imag
Page 11 and 12: Chapter 1 Introduction The developm
Page 13 and 14: Figure 1.3: This thesis combines fi
Page 15: the presentation of the stochastic
Page 18 and 19: Chapter 2 Image Segmentation and Li
Page 36 and 37: Chapter 3 SPDEs and Polynomial Chao
Page 48 and 49: Chapter 4 Discretization of SPDEs F
Page 50 and 51: Chapter 4 Discretization of SPDEs 4
Page 52 and 53: Chapter 4 Discretization of SPDEs a
Page 58 and 59: Chapter 5 Stochastic Images
Page 60 and 61: Chapter 5 Stochastic Images Figure
Page 62 and 63: Chapter 5 Stochastic Images like qu
Page 64 and 65: Chapter 5 Stochastic Images Figure
Page 67 and 68: Chapter 6 Segmentation of Stochasti
Page 69 and 70: 6.1 Random Walker Segmentation on S
Page 77 and 78: 6.2 Ambrosio-Tortorelli Segmentatio
Page 87: 6.2 Ambrosio-Tortorelli Segmentatio
Page 90 and 91: Chapter 7 Stochastic Level Sets whe
Page 92 and 93: Chapter 7 Stochastic Level Sets Fig
Page 94 and 95: Chapter 7 Stochastic Level Sets and
Page 96 and 97:
Chapter 7 Stochastic Level Sets rar
Page 98 and 99:
Chapter 7 Stochastic Level Sets Fig
Page 100 and 101:
Chapter 7 Stochastic Level Sets MC
Page 102 and 103:
Page 104 and 105:
Page 106 and 107:
Chapter 7 Stochastic Level Sets act
Page 108 and 109:
Chapter 8 Segmentation of Classical
Page 110 and 111:
Page 112 and 113:
Page 114 and 115:
Page 116 and 117:
Page 118 and 119:
Chapter 9 Summary, Discussion, and
Page 121 and 122:
List of Figures 1.1 Left: CT image
Page 123 and 124:
List of Figures 6.2 Mean and varian
Page 125:
List of Figures 7.12 Mean (left) of
Page 129 and 130:
Appendix A Publications Written Dur
Page 131 and 132:
Bibliography [14] L. Ambrosio and M
Page 133 and 134:
Bibliography [46] B. Echebarria, R.
Page 135 and 136:
Bibliography [81] B. N. Khoromskij
Page 137 and 138:
Bibliography [113] A. Nouy. A gener
Page 139:
Bibliography [147] J. Tryoen, O. Le
show all

Segmentation of Stochastic Images using ... - Jacobs University

Create successful ePaper yourself

Delete template?

Save as template?