Mathematics in Independent Component Analysis

1.2. Uniqueness issues in independent component analysis 9
f 1, f 2
2
1.5
1
0.5
-2 -1.5 -1 -0.5
-0.5
0.5 1 1.5 2
-1
-1.5
-2
1
0.5
0
-0.5
-1
f (As ) A − 1 f (As )
0.5 1 1.5
0.5 1 1.5
1
0.5
0
-0.5
-1
1
0.8
0.6
0.4
0.2
0
0.2 0.4 0.6 0.8
0.2 0.4 0.6 0.8
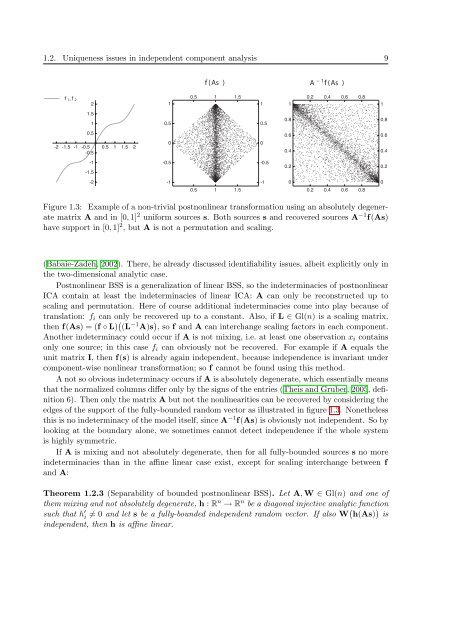
Figure 1.3: Example of a non-trivial postnonlinear transformation using an absolutely degenerate
matrix A and in [0, 1] 2 uniform sources s. Both sources s and recovered sources A −1 f(As)
have support in [0, 1] 2 , but A is not a permutation and scaling.
(Babaie-Zadeh, 2002). There, he already discussed identifiability issues, albeit explicitly only in
the two-dimensional analytic case.
Postnonlinear BSS is a generalization of linear BSS, so the indeterminacies of postnonlinear
ICA contain at least the indeterminacies of linear ICA: A can only be reconstructed up to
scaling and permutation. Here of course additional indeterminacies come into play because of
translation: fi can only be recovered up to a constant. Also, if L ∈ Gl(n) is a scaling matrix,
then f(As) = (f ◦ L) � (L −1 A)s � , so f and A can interchange scaling factors in each component.
Another indeterminacy could occur if A is not mixing, i.e. at least one observation xi contains
only one source; in this case fi can obviously not be recovered. For example if A equals the
unit matrix I, then f(s) is already again independent, because independence is invariant under
component-wise nonlinear transformation; so f cannot be found using this method.
A not so obvious indeterminacy occurs if A is absolutely degenerate, which essentially means
that the normalized columns differ only by the signs of the entries (Theis and Gruber, 2005, definition
6). Then only the matrix A but not the nonlinearities can be recovered by considering the
edges of the support of the fully-bounded random vector as illustrated in figure 1.3. Nonetheless
this is no indeterminacy of the model itself, since A −1 f(As) is obviously not independent. So by
looking at the boundary alone, we sometimes cannot detect independence if the whole system
is highly symmetric.
If A is mixing and not absolutely degenerate, then for all fully-bounded sources s no more
indeterminacies than in the affine linear case exist, except for scaling interchange between f
and A:
Theorem 1.2.3 (Separability of bounded postnonlinear BSS). Let A, W ∈ Gl(n) and one of
them mixing and not absolutely degenerate, h : R n → R n be a diagonal injective analytic function
such that h ′ i �= 0 and let s be a fully-bounded independent random vector. If also W� h(As) � is
independent, then h is affine linear.
1
0.8
0.6
0.4
0.2
0