- Page 1 and 2:
Statistical machine learning of bio
- Page 3:
to Jakob
- Page 6 and 7:
vi Preface
- Page 8 and 9:
viii CONTENTS 3 Signal Processing 8
- Page 11 and 12:
Chapter 1 Statistical machine learn
- Page 13 and 14:
1.1. Introduction 5 auditory cortex
- Page 15 and 16:
1.2. Uniqueness issues in independe
- Page 17 and 18:
1.2. Uniqueness issues in independe
- Page 19 and 20:
S U M M A R Y T his �le contains
- Page 21 and 22:
1.3. Dependent component analysis 1
- Page 23 and 24:
Table 1.1: BSS algorithms based on
- Page 25 and 26:
1.3. Dependent component analysis 1
- Page 27 and 28:
1.3. Dependent component analysis 1
- Page 29 and 30:
1.3. Dependent component analysis 2
- Page 31 and 32:
1.3. Dependent component analysis 2
- Page 33 and 34:
1.4. Sparseness 25 1.4 Sparseness O
- Page 35 and 36:
1.4. Sparseness 27 Theorem 1.4.3 (S
- Page 37 and 38:
1.4. Sparseness 29 R 3 R 3 A BSRA R
- Page 39 and 40:
1.4. Sparseness 31 Sparse projectio
- Page 41 and 42:
1.5. Machine learning for data prep
- Page 43 and 44:
1.5. Machine learning for data prep
- Page 45 and 46:
1.5. Machine learning for data prep
- Page 47 and 48:
1.5. Machine learning for data prep
- Page 49 and 50:
1.5. Machine learning for data prep
- Page 51 and 52:
1.6. Applications to biomedical dat
- Page 53 and 54:
1.6. Applications to biomedical dat
- Page 55 and 56:
1.6. Applications to biomedical dat
- Page 57 and 58:
1.6. Applications to biomedical dat
- Page 59 and 60:
1.7. Outlook 51 noise data signal i
- Page 61:
Part II Papers 53
- Page 64 and 65:
56 Chapter 2. Neural Computation 16
- Page 66 and 67:
58 Chapter 2. Neural Computation 16
- Page 68 and 69:
60 Chapter 2. Neural Computation 16
- Page 70 and 71:
62 Chapter 2. Neural Computation 16
- Page 72 and 73:
64 Chapter 2. Neural Computation 16
- Page 74 and 75:
66 Chapter 2. Neural Computation 16
- Page 76 and 77:
68 Chapter 2. Neural Computation 16
- Page 78 and 79:
70 Chapter 2. Neural Computation 16
- Page 80 and 81:
72 Chapter 2. Neural Computation 16
- Page 82 and 83:
74 Chapter 2. Neural Computation 16
- Page 84 and 85:
76 Chapter 2. Neural Computation 16
- Page 86 and 87:
78 Chapter 2. Neural Computation 16
- Page 88 and 89:
80 Chapter 2. Neural Computation 16
- Page 90 and 91:
82 Chapter 3. Signal Processing 84(
- Page 92 and 93:
84 Chapter 3. Signal Processing 84(
- Page 94 and 95:
86 Chapter 3. Signal Processing 84(
- Page 96 and 97:
88 Chapter 3. Signal Processing 84(
- Page 98 and 99:
90 Chapter 4. Neurocomputing 64:223
- Page 100 and 101:
92 Chapter 4. Neurocomputing 64:223
- Page 102 and 103:
94 Chapter 4. Neurocomputing 64:223
- Page 104 and 105:
96 Chapter 4. Neurocomputing 64:223
- Page 106 and 107:
98 Chapter 4. Neurocomputing 64:223
- Page 108 and 109:
100 Chapter 4. Neurocomputing 64:22
- Page 110 and 111:
102 Chapter 4. Neurocomputing 64:22
- Page 112 and 113:
104 Chapter 5. IEICE TF E87-A(9):23
- Page 114 and 115:
106 Chapter 5. IEICE TF E87-A(9):23
- Page 116 and 117:
108 Chapter 5. IEICE TF E87-A(9):23
- Page 118 and 119:
110 Chapter 5. IEICE TF E87-A(9):23
- Page 120 and 121:
112 Chapter 5. IEICE TF E87-A(9):23
- Page 122 and 123:
114 Chapter 6. LNCS 3195:726-733, 2
- Page 124 and 125:
116 Chapter 6. LNCS 3195:726-733, 2
- Page 126 and 127:
118 Chapter 6. LNCS 3195:726-733, 2
- Page 128 and 129:
120 Chapter 6. LNCS 3195:726-733, 2
- Page 130 and 131:
122 Chapter 6. LNCS 3195:726-733, 2
- Page 132 and 133:
124 Chapter 7. Proc. ISCAS 2005, pa
- Page 134 and 135:
126 Chapter 7. Proc. ISCAS 2005, pa
- Page 136 and 137:
128 Chapter 7. Proc. ISCAS 2005, pa
- Page 138 and 139:
130 Chapter 8. Proc. NIPS 2006 Towa
- Page 140 and 141:
132 Chapter 8. Proc. NIPS 2006 1.3
- Page 142 and 143:
134 Chapter 8. Proc. NIPS 2006 stru
- Page 144 and 145:
136 Chapter 8. Proc. NIPS 2006 5.5
- Page 146 and 147:
138 Chapter 8. Proc. NIPS 2006
- Page 148 and 149:
140 Chapter 9. Neurocomputing (in p
- Page 150 and 151:
142 Chapter 9. Neurocomputing (in p
- Page 152 and 153:
144 Chapter 9. Neurocomputing (in p
- Page 154 and 155:
146 Chapter 9. Neurocomputing (in p
- Page 156 and 157:
148 Chapter 9. Neurocomputing (in p
- Page 158 and 159:
150 Chapter 9. Neurocomputing (in p
- Page 160 and 161:
152 Chapter 9. Neurocomputing (in p
- Page 162 and 163:
154 Chapter 9. Neurocomputing (in p
- Page 164 and 165:
156 Chapter 10. IEEE TNN 16(4):992-
- Page 166 and 167:
158 Chapter 10. IEEE TNN 16(4):992-
- Page 168 and 169:
160 Chapter 10. IEEE TNN 16(4):992-
- Page 170 and 171:
162 Chapter 11. EURASIP JASP, 2007
- Page 172 and 173:
164 Chapter 11. EURASIP JASP, 2007
- Page 174 and 175:
166 Chapter 11. EURASIP JASP, 2007
- Page 176 and 177:
168 Chapter 11. EURASIP JASP, 2007
- Page 178 and 179:
170 Chapter 11. EURASIP JASP, 2007
- Page 180 and 181:
172 Chapter 11. EURASIP JASP, 2007
- Page 182 and 183:
174 Chapter 11. EURASIP JASP, 2007
- Page 184 and 185:
176 Chapter 12. LNCS 3195:718-725,
- Page 186 and 187:
178 Chapter 12. LNCS 3195:718-725,
- Page 188 and 189:
180 Chapter 12. LNCS 3195:718-725,
- Page 190 and 191:
182 Chapter 12. LNCS 3195:718-725,
- Page 192 and 193:
184 Chapter 12. LNCS 3195:718-725,
- Page 194 and 195:
186 Chapter 13. Proc. EUSIPCO 2005
- Page 196 and 197:
188 Chapter 13. Proc. EUSIPCO 2005
- Page 198 and 199:
190 Chapter 13. Proc. EUSIPCO 2005
- Page 200 and 201:
192 Chapter 14. Proc. ICASSP 2006 S
- Page 202 and 203:
194 Chapter 14. Proc. ICASSP 2006 A
- Page 204 and 205:
196 Chapter 14. Proc. ICASSP 2006
- Page 206 and 207:
198 Chapter 15. Neurocomputing, 69:
- Page 208 and 209:
200 Chapter 15. Neurocomputing, 69:
- Page 210 and 211:
202 Chapter 15. Neurocomputing, 69:
- Page 212 and 213:
204 Chapter 15. Neurocomputing, 69:
- Page 214 and 215:
206 Chapter 15. Neurocomputing, 69:
- Page 216 and 217:
208 Chapter 15. Neurocomputing, 69:
- Page 218 and 219:
210 Chapter 15. Neurocomputing, 69:
- Page 220 and 221:
212 Chapter 15. Neurocomputing, 69:
- Page 222 and 223:
214 Chapter 15. Neurocomputing, 69:
- Page 224 and 225:
216 Chapter 15. Neurocomputing, 69:
- Page 226 and 227:
218 Chapter 15. Neurocomputing, 69:
- Page 228 and 229:
220 Chapter 15. Neurocomputing, 69:
- Page 230 and 231:
222 Chapter 15. Neurocomputing, 69:
- Page 232 and 233:
224 Chapter 15. Neurocomputing, 69:
- Page 234 and 235:
226 Chapter 15. Neurocomputing, 69:
- Page 236 and 237: 228 Chapter 15. Neurocomputing, 69:
- Page 238 and 239: 230 Chapter 16. Proc. ICA 2006, pag
- Page 240 and 241: 232 Chapter 16. Proc. ICA 2006, pag
- Page 242 and 243: 234 Chapter 16. Proc. ICA 2006, pag
- Page 244 and 245: 236 Chapter 16. Proc. ICA 2006, pag
- Page 246 and 247: 238 Chapter 16. Proc. ICA 2006, pag
- Page 248 and 249: 240 Chapter 17. IEEE SPL 13(2):96-9
- Page 250 and 251: 242 Chapter 17. IEEE SPL 13(2):96-9
- Page 252 and 253: 244 Chapter 17. IEEE SPL 13(2):96-9
- Page 254 and 255: 246 Chapter 18. Proc. EUSIPCO 2006
- Page 256 and 257: 248 Chapter 18. Proc. EUSIPCO 2006
- Page 258 and 259: 250 Chapter 18. Proc. EUSIPCO 2006
- Page 260 and 261: 252 Chapter 19. LNCS 3195:977-984,
- Page 262 and 263: 254 Chapter 19. LNCS 3195:977-984,
- Page 264 and 265: 256 Chapter 19. LNCS 3195:977-984,
- Page 266 and 267: 258 Chapter 19. LNCS 3195:977-984,
- Page 268 and 269: 260 Chapter 19. LNCS 3195:977-984,
- Page 270 and 271: 262 Chapter 20. Signal Processing 8
- Page 272 and 273: 264 Chapter 20. Signal Processing 8
- Page 274 and 275: 266 Chapter 20. Signal Processing 8
- Page 276 and 277: 268 Chapter 20. Signal Processing 8
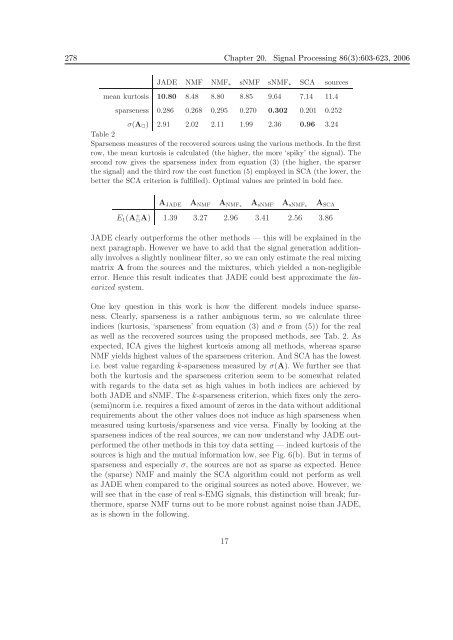
- Page 278 and 279: 270 Chapter 20. Signal Processing 8
- Page 280 and 281: 272 Chapter 20. Signal Processing 8
- Page 282 and 283: 274 Chapter 20. Signal Processing 8
- Page 284 and 285: 276 Chapter 20. Signal Processing 8
- Page 288 and 289: 280 Chapter 20. Signal Processing 8
- Page 290 and 291: 282 Chapter 20. Signal Processing 8
- Page 292 and 293: 284 Chapter 20. Signal Processing 8
- Page 294 and 295: 286 Chapter 20. Signal Processing 8
- Page 296 and 297: 288 Chapter 20. Signal Processing 8
- Page 298 and 299: 290 Chapter 20. Signal Processing 8
- Page 300 and 301: 292 Chapter 21. Proc. BIOMED 2005,
- Page 302 and 303: 294 Chapter 21. Proc. BIOMED 2005,
- Page 304 and 305: 296 Chapter 21. Proc. BIOMED 2005,
- Page 306 and 307: 298 BIBLIOGRAPHY Barber, C., Dobkin
- Page 308 and 309: 300 BIBLIOGRAPHY Georgiev, P. (2001
- Page 310 and 311: 302 BIBLIOGRAPHY Keck, I., Theis, F
- Page 312 and 313: 304 BIBLIOGRAPHY Schießl, I., Sch
- Page 314 and 315: 306 BIBLIOGRAPHY Theis, F. and Inou