Third Day Poster Session, 17 June 2010 - NanoTR-VI

P
is
P
P
is
is
is
P,P
is
Poster Session, Thursday, June 17
Theme F686 - N1123
Photoluminescent Properties of InN Thin Films
1
2
1
2
1
2
3
3
UÖ. DönmezUP P*, M. YlmazP P, A. ErolP P, B. UluP P, M.Ç. ArkanP P, A. UluP
PA. O. AjagunnaP P, E. IliopoulosP P, A. GeorgakilasP
1
PIstanbul University, Science Faculty, Department of Physics 34134 Vezneciler, Istanbul, Turkey
2
PAkdeniz University, Faculty of Arts & Science, Department of Physics, Antalya, Turkey
PMicroelectronics Research Group, IESL, FORTH and Physics Department, University of Crete, P.O. Box 1385, 71110 Heraklion-Crete, Greece
3
Abstract-We report photoluminescence (PL) studies of InN epilayers grown by plasma-assisted molecular beam epitaxy with free-electron
19 -3
concentration of about 10P
PcmP P. Band gap of InN layer is determined using the PL data obtained as a function of temperature and is calculated
by a model considering the high electron concentration effect, electron-electron and electron-ionized impurity interactions in non-parabolic k·p
model. PL results indicate that the band gap of InN is 0.82eV at 8K. Electron effective mass is calculated as 0.097mR0 Rfor electron concentration
19 -3
of 10P
PcmP
3
InN is in nature n-type semiconductor having free-electron
21 -3
concentrations as high as 10P
PcmP
P. Early studies of the
interband optical absorption carried out on InN thin films have
shown that band gap energy is about 2eV due to high carrier
concentration effects [1-2]. Recent studies showed that the
band gap energy is about 0.65eV [3-6]. This means that using
group InN and In-rich InGaN have potential to optoelectronic
devices covering the spectrum from infrared to ultraviolet.
In this study, Hall effect measurement has employed to
determine carrier concentration for two samples having
different InN layer thicknesses as shown in Figure 1.
Carrier Conc.(cm -3 )
1,4E19
1,3E19
1,2E19
1,1E19
800nm InN layer
600nm InN layer
1E19
60 90 120 150 180 210 240 270 300
Temperature (K)
Figure 1. Temperature dependence of carrier concentration of 800 nm
and 600 nm thick InN layers
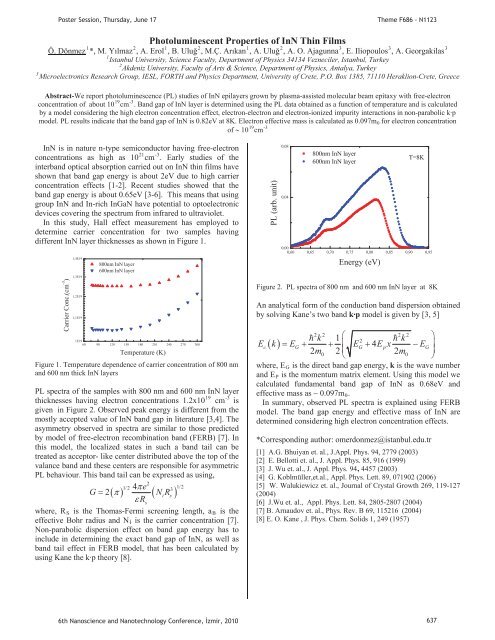
PL spectra of the samples with 800 nm and 600 nm InN layer
19 -3
thicknesses having electron concentrations 1.2x10P
P cmP
Pis
given in Figure 2. Observed peak energy is different from the
mostly accepted value of InN band gap in literature [3,4]. The
asymmetry observed in spectra are similar to those predicted
by model of free-electron recombination band (FERB) [7]. In
this model, the localized states in such a band tail can be
treated as acceptor- like center distributed above the top of the
valance band and these centers are responsible for asymmetric
PL behaviour. This band tail can be expressed as using,
2
1/2 4
e 3
1/2
G 2
NiR
s
Rs
where, RRSR the Thomas-Fermi screening length, aRBR the
effective Bohr radius and NRR the carrier concentration [7].
Non-parabolic dispersion effect on band gap energy has to
include in determining the exact band gap of InN, as well as
band tail effect in FERB model, that has been calculated by
using Kane the k·p theory [8].
PL (arb. unit)
0,08
0,04
800nm InN layer
600nm InN layer
0,00
0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95
Energy (eV)
T=8K
Figure 2. PL spectra of 800 nm and 600 nm InN layer at 8K
An analytical form of the conduction band dispersion obtained
by solving Kane’s two band k·p model is given by [3, 5]
2 2 2 2
k 1
2 k
Eck EG EG 4Epx EG
2m0 2
2m
0
where, ERGR the direct band gap energy, k is the wave number
and ERPR the momentum matrix element. Using this model we
calculated fundamental band gap of InN as 0.68eV and
effective mass as ~ 0.097mR0R.
In summary, observed PL spectra is explained using FERB
model. The band gap energy and effective mass of InN are
determined considering high electron concentration effects.
*Corresponding author: omerdonmez@istanbul.edu.tr
[1] A.G. Bhuiyan et. al., J.Appl. Phys. 94, 2779 (2003)
[2] E. Bellotti et. al., J. Appl. Phys. 85, 916 (1999)
[3] J. Wu et. al., J. Appl. Phys. T94T, 4457 (2003)
[4] G. Koblmüller,et.al., Appl. Phys. Lett. 89, 071902 (2006)
[5] W. Walukiewicz et. al., Journal of Crystal Growth 269, 119-127
(2004)
[6] J.Wu et. al., Appl. Phys. Lett. 84, 2805-2807 (2004)
[7] B. Arnaudov et. al., Phys. Rev. B 69, 115216 (2004)
[8] E. O. Kane , J. Phys. Chem. Solids 1, 249 (1957)
6th Nanoscience and Nanotechnology Conference, zmir, 2010 637