Photonic crystals in biology

Poster Session, Tuesday, June 15
Theme A1 - B702
Investigating the Temperature Effect on Velocity Profile in Electroosmotics Driven Nano-Channel
Mehdi Mostofi 1 *, Davood D. Ganji 2 and Mofid Gorji-Bandpy 2
1 Islamic Azad University, East Tehran Branch, Tehran, Iran.
2 Department of Mechanical Engineering, Noshiravani University of Technology, Babol, Iran
Abstract-In this paper, an electroosmotic flow of an electrolyte in a 15 nm radius nano-channe l will be investigated. This study will be with
existence of the Electric Double Layer (EDL) with large zeta potentials. In large amounts of zeta potential, numerical study should be employed
in order to investigate the flow field. Governing equations for electroosmotic phenomena are Poisson-Boltzmann, Navier-Stokes, species and
mass conservation equations. In most of the literature surveyed works, all physical properties are assumed to be constant, but in this paper,
temperature will be variable and consequently, some of the fluid properties such as dielectric constant and dynamic viscosity are not constant as
well. After modeling the variations of the fluid properties through temperature, velocity is investigated in some typical temperatures.
Nano-channel term is referred to channels with hydraulic
diameter less than 100 nanometers [1].
Concentrating surface loads in liquid – solid interface makes
the EDL to be existed in electroosmotic phenomena. If the
loads are concentrated in the end of nano-channels, a potential
difference will be generated that forces the ions in the nanochannel.
However, induced electric field is discharged by
electric conduction of the electrolyte.
Rice and Whitehead [2], Lu and Chan [3] and Ke and Liu
[4] studied the flow in capillary tube. None of them solved the
problem based on the curvilinear coordinates system. Also, all
of them studied the problem with existence of the pressure
gradient while in the modern applications, the pressure
gradient can be eliminated and consequently, solving the
problem considering this fact is necessary. In this paper,
velocity profiles for large zeta potentials without pressure
gradient will be studied based on the curvilinear coordinates in
a capillary tube.
Governing equations in electroosmotic phenomena are
species and mass conservation, Navier-Stokes and Poisson-
Boltzmann equations [5]. By some simplifications, set of
nonlinear differential equations will be identified for bulk
flu id:
1
r
X p
X m
2
(1)
r r
r
1 u
e
E0
RT
r
X
p
X
m
2
(2)
r r
r
F U
0
According to [5], we can explore the following assumption for
nano-tube bulk fluid:
1
sinh
r
2
(3)
r r
r
In small amount of zeta potential, we can assume sinh
and consequently, problem will be solved analytically, but in
this paper, this assumption is no longer valid. As a result,
numerical simulation has been employed. By using finite
difference method powered by Newton-Raphson algorithm,
flow and velocity fields have been obtained through nanotube.
Next, the main part of the paper contribution starts.
Temperature assumed to be variable in the range of liquid
water (0 to 100 o C). in this case, some of the electrolyte
(water) properties will be variable such as viscosity and
dielectric constant . in addition, zeta potential is affected by
e
temperature variations. In this paper, we use the exact
definition or interpolation for temperature effect on zeta
potential, dynamic viscosity and dielectric constant according
to data shown in [5,6,7] respectively.
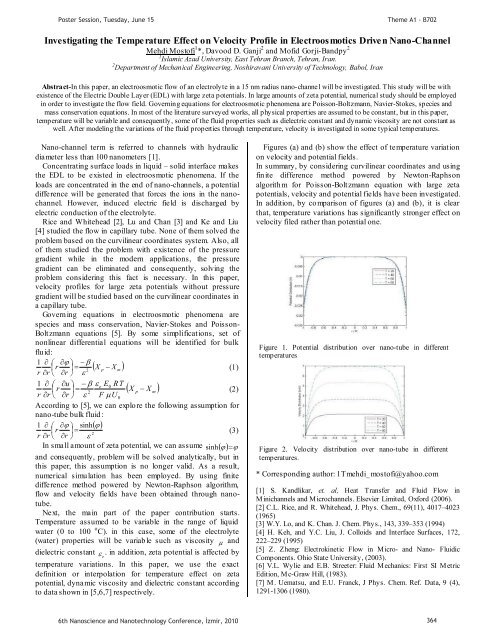
Figures (a) and (b) show the effect of temperature variation
on velocity and potential fields.
In summary, by considering curvilinear coordinates and using
finite difference method powered by Newton-Raphson
algorithm for Poisson-Boltzmann equation with large zeta
potentials, velocity and potential fields have been investigated.
In addition, by comparison of figures (a) and (b), it is clear
that, temperature variations has significantly stronger effect on
velocity filed rather than potential one.
Figure 1. Potential distribution over nano-tube in different
temperatures
Figure 2. Velocity distribution over nano-tube in different
temperatures.
* Corresponding author: 1Tmehdi_mostofi@yahoo.com
[1] S. Kandlikar, et. al, Heat Transfer and Fluid Flow in
Minichannels and Microchannels. Elsevier Limited, Oxford (2006).
[2] C.L. Rice, and R. Whitehead, J. Phys. Chem., 69(11), 4017–4023
(1965)
[3] W.Y. Lo, and K. Chan. J. Chem. Phys., 143, 339–353 (1994)
[4] H. Keh, and Y.C. Liu, J. Colloids and Interface Surfaces, 172,
222–229 (1995)
[5] Z. Zheng: Electrokinetic Flow in Micro- and Nano- Fluidic
Components. Ohio State University, (2003).
[6] V.L. Wylie and E.B. Streeter: Fluid Mechanics: First SI Metric
Edition, Mc-Graw Hill, (1983).
[7] M. Uematsu, and E.U. Franck, J Phys. Chem. Ref. Data, 9 (4),
1291-1306 (1980).
6th Nanoscience and Nanotechnology Conference, zmir, 2010 364