PPKE ITK PhD and MPhil Thesis Classes

More documents

Recommendations

Info

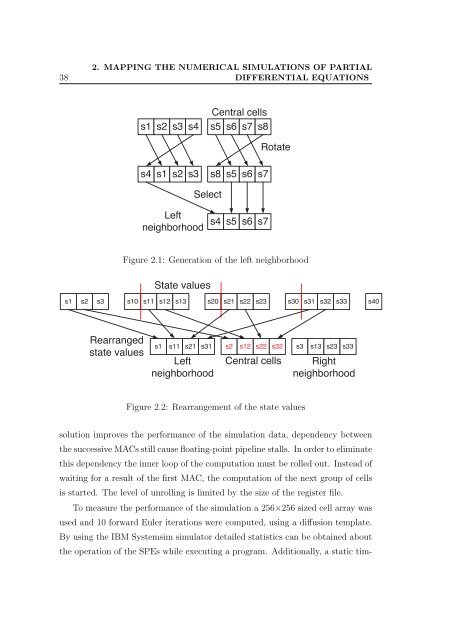
38 2. MAPPING THE NUMERICAL SIMULATIONS OF PARTIAL DIFFERENTIAL EQUATIONS s1 s2 s3 s4 Central cells s5 s6 s7 s8 Rotate s4 s1 s2 s3 s8 s5 s6 s7 Select Left neighborhood s4 s5 s6 s7 Figure 2.1: Generation of the left neighborhood State values s1 s2 s3 s10 s11 s12 s13 s20 s21 s22 s23 s30 s31 s32 s33 s40 Rearranged state values s1 s11 s21 s31 s2 s12 s22 s32 s3 s13 s23 s33 Left neighborhood Central cells Right neighborhood Figure 2.2: Rearrangement of the state values solution improves the performance of the simulation data, dependency between the successive MACs still cause floating-point pipeline stalls. In order to eliminate this dependency the inner loop of the computation must be rolled out. Instead of waiting for a result of the first MAC, the computation of the next group of cells is started. The level of unrolling is limited by the size of the register file. To measure the performance of the simulation a 256×256 sized cell array was used and 10 forward Euler iterations were computed, using a diffusion template. By using the IBM Systemsim simulator detailed statistics can be obtained about the operation of the SPEs while executing a program. Additionally, a static tim-
2.1 Introduction 39 Instruction historgram 1.50E+07 1.13E+07 7.50E+06 3.75E+06 0E+00 UR0 UR2 UR4 UR8 Single cycle Dual cycle Nop cycle Stall due to branch miss Stall due to prefetch miss Stall due to dependency Stall due to fp resource conflict Stall due to waiting for hint target Stall due to dp pipeline Channel stall cycle SPU Initialization cycle Number of Instructions Figure 2.3: Results of the loop unrolling ing of the program can be created where the pipeline stalls can be identified. The instruction histogram is shown in Figure 2.3. Without unrolling, more than 13 million clock cycles are required to complete the computation and the utilization of the SPE is only 35%. Most of the time, the SPE is stalled, due to data dependency between the successive MAC operations. By unrolling the inner loop of the computation and computing 2, 4 or 8 sets of cells, with the cost of larger area, most of the pipeline stall cycles can be eliminated and the required clock cycles can be reduced to 3.5 million. When the inner loop of the computation is unrolled 8 times the efficiency of the SPE can be increased to 90%. Performance of one SPE in the computation of the CNN dynamics is 624 million cell iteration/s. As shown in Figure 2.4. the SPE is nearly one order faster than a high performance desktop microprocessor. The Falcon processor can outperform the Cell if it is implemented on a large FPGA. On a Xilinx Virtex-5 SX95T more than 70 Falcon PE can be implemented. To achieve even faster computation multiple SPEs can be used. The data can be partitioned between the SPEs by horizontally striping the CNN cell array. The
Page 1:
An Optimal Mapping of Numerical Sim
Page 5 and 6:
Acknowledgements It is not so hard
Page 7 and 8: Contents 1 Introduction 1 1.1 Cellu
Page 9: CONTENTS iii 4.3.3 Operating Steps
Page 12 and 13: vi LIST OF FIGURES 2.4 Performance
Page 15: List of Tables 2.1 Comparison of di
Page 18 and 19: xii LIST OF ABBREVIATIONS FPE Falco
Page 21 and 22: Chapter 1 Introduction Due to the r
Page 23 and 24: 3 can be represented in arbitrary t
Page 25 and 26: 1.1 Cellular Neural/Nonlinear Netwo
Page 27 and 28: 1.2 Cellular Neural/Nonlinear Netwo
Page 29 and 30: 1.3 CNN-UM Implementations 9 the Lo
Page 31 and 32: 1.3 CNN-UM Implementations 11 modif
Page 33 and 34: 1.4 Field Programmable Gate Arrays
Page 47 and 48: 1.5 IBM Cell Broadband Engine Archi
Page 55 and 56: Chapter 2 Mapping the Numerical Sim
Page 57: 2.1 Introduction 37 18 Load instruc
Page 61 and 62: 2.1 Introduction 41 2E+07 1E+07 9E+
Page 63 and 64: 2.1 Introduction 43 Main memory 8 t
Page 65 and 66: 2.1 Introduction 45 6 4.5 3 Speedup
Page 67 and 68: 2.1 Introduction 47 2.50E+07 1.88E+
Page 69 and 70: 2.2 Ocean model and its implementat
Page 71 and 72: 2.2 Ocean model and its implementat
Page 73 and 74: 2.3 Computational Fluid Flow Simula
Page 89 and 90: Chapter 3 Investigating the Precisi
Page 91 and 92: 3.2 Numerical Solutions of the PDEs
Page 93 and 94: 3.3 Testing Methodology 73 In fixed
Page 95 and 96: 3.4 Properties of the Arithmetic Un
Page 97 and 98: 3.4 Properties of the Arithmetic Un
Page 99 and 100: 3.5 Results 79 in the L2 cache of t
Page 101 and 102: 3.5 Results 81 1E-02 1E-03 Error 1E
Page 103 and 104: 3.5 Results 83 arithmetic unit requ
Page 105: 3.6 Conclusion 85 point and the 40
Page 108 and 109:
4. IMPLEMENTING A GLOBAL ANALOGIC P
Page 110 and 111:
Page 112 and 113:
Page 114 and 115:
Page 116 and 117:
Page 118 and 119:
Page 120 and 121:
Page 122 and 123:
Page 124 and 125:
Page 126 and 127:
Page 128 and 129:
Page 130 and 131:
110 5. SUMMARY OF NEW SCIENTIFIC RE
Page 132 and 133:
Page 134 and 135:
Page 136 and 137:
Page 138 and 139:
Page 141 and 142:
References The author’s journal p
Page 143 and 144:
5.2 Application of the results 123
Page 145 and 146:
Page 147 and 148:
show all

PPKE ITK PhD and MPhil Thesis Classes

Create successful ePaper yourself

Delete template?

Save as template?