Lenses and Waves
Lenses and Waves
Lenses and Waves
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
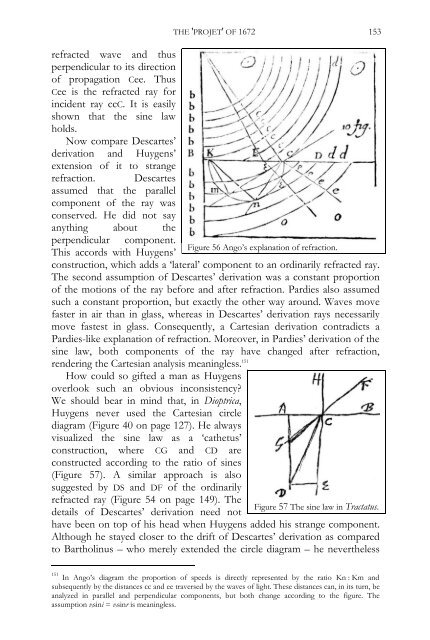
efracted wave <strong>and</strong> thus<br />
perpendicular to its direction<br />
of propagation Cee. Thus<br />
Cee is the refracted ray for<br />
incident ray ccC. It is easily<br />
shown that the sine law<br />
holds.<br />
Now compare Descartes’<br />
derivation <strong>and</strong> Huygens’<br />
extension of it to strange<br />
refraction. Descartes<br />
assumed that the parallel<br />
component of the ray was<br />
conserved. He did not say<br />
anything about the<br />
perpendicular component.<br />
This accords with Huygens’<br />
THE 'PROJET' OF 1672 153<br />
construction, which adds a ‘lateral’ component to an ordinarily refracted ray.<br />
The second assumption of Descartes’ derivation was a constant proportion<br />
of the motions of the ray before <strong>and</strong> after refraction. Pardies also assumed<br />
such a constant proportion, but exactly the other way around. <strong>Waves</strong> move<br />
faster in air than in glass, whereas in Descartes’ derivation rays necessarily<br />
move fastest in glass. Consequently, a Cartesian derivation contradicts a<br />
Pardies-like explanation of refraction. Moreover, in Pardies’ derivation of the<br />
sine law, both components of the ray have changed after refraction,<br />
rendering the Cartesian analysis meaningless. 151<br />
How could so gifted a man as Huygens<br />
overlook such an obvious inconsistency?<br />
We should bear in mind that, in Dioptrica,<br />
Huygens never used the Cartesian circle<br />
diagram (Figure 40 on page 127). He always<br />
visualized the sine law as a ‘cathetus’<br />
construction, where CG <strong>and</strong> CD are<br />
constructed according to the ratio of sines<br />
(Figure 57). A similar approach is also<br />
suggested by DS <strong>and</strong> DF of the ordinarily<br />
refracted ray (Figure 54 on page 149). The<br />
details of Descartes’ derivation need not<br />
Figure 56 Ango’s explanation of refraction.<br />
Figure 57 The sine law in Tractatus.<br />
have been on top of his head when Huygens added his strange component.<br />
Although he stayed closer to the drift of Descartes’ derivation as compared<br />
to Bartholinus – who merely extended the circle diagram – he nevertheless<br />
151 In Ango’s diagram the proportion of speeds is directly represented by the ratio Kn : Km <strong>and</strong><br />
subsequently by the distances cc <strong>and</strong> ee traversed by the waves of light. These distances can, in its turn, be<br />
analyzed in parallel <strong>and</strong> perpendicular components, but both change according to the figure. The<br />
assumption visini = vrsinr is meaningless.