- Page 2 and 3: Archimedes Volume 9
- Page 4 and 5: Lenses and Waves Christiaan Huygens
- Page 6 and 7: Contents CHAPTER 1 INTRODUCTION -
- Page 8 and 9: CONTENTS vii Hobbes, Hooke and the
- Page 10 and 11: Preface “Le doute fait peine a l
- Page 12 and 13: Chapter 1 Introduction - ‘the per
- Page 14 and 15: ‘THE PERFECT CARTESIAN’ 3 first
- Page 16 and 17: ‘THE PERFECT CARTESIAN’ 5 was t
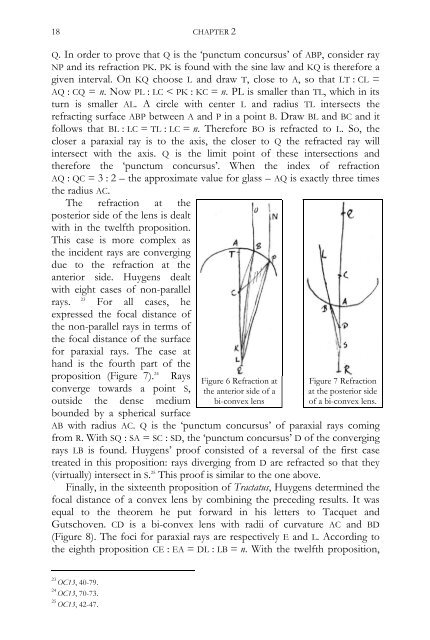
- Page 18 and 19: ‘THE PERFECT CARTESIAN’ 7 merel
- Page 20 and 21: ‘THE PERFECT CARTESIAN’ 9 concl
- Page 22 and 23: Chapter 2 1653 - 'Tractatus' The ma
- Page 24 and 25: 1653 - TRACTATUS 13 images. In La D
- Page 26 and 27: 1653 - TRACTATUS 15 Huygens launche
- Page 30 and 31: 1653 - TRACTATUS 19 the ‘punctum
- Page 32 and 33: 1653 - TRACTATUS 21 lens ACB and it
- Page 34 and 35: 1653 - TRACTATUS 23 object should l
- Page 36 and 37: 1653 - TRACTATUS 25 development of
- Page 38 and 39: 1653 - TRACTATUS 27 when in 1600 he
- Page 40 and 41: 1653 - TRACTATUS 29 chapter of Para
- Page 42 and 43: 1653 - TRACTATUS 31 incidence; the
- Page 44 and 45: 1653 - TRACTATUS 33 focused on prob
- Page 46 and 47: 1653 - TRACTATUS 35 fancied - he re
- Page 48 and 49: 1653 - TRACTATUS 37 magnification,
- Page 50 and 51: 1653 - TRACTATUS 39 remaining uncom
- Page 52 and 53: 1653 - TRACTATUS 41 equation. 111 D
- Page 54 and 55: 1653 - TRACTATUS 43 exact descripti
- Page 56 and 57: 1653 - TRACTATUS 45 measurements re
- Page 58 and 59: 1653 - TRACTATUS 47 insertion of a
- Page 60 and 61: 1653 - TRACTATUS 49 images of exten
- Page 62 and 63: 1653 - TRACTATUS 51 expect that the
- Page 64 and 65: Chapter 3 1655-1672 - 'De Aberratio
- Page 66 and 67: 1655-1672 - DE ABERRATIONE 55 chapt
- Page 68 and 69: 1655-1672 - DE ABERRATIONE 57 remai
- Page 70 and 71: 1655-1672 - DE ABERRATIONE 59 techn
- Page 72 and 73: 1655-1672 - DE ABERRATIONE 61 well
- Page 74 and 75: 1655-1672 - DE ABERRATIONE 63 impro
- Page 76 and 77: 1655-1672 - DE ABERRATIONE 65 “Al
- Page 78 and 79:
1655-1672 - DE ABERRATIONE 67 lense
- Page 80 and 81:
TS = 7 BG, where BG is the thicknes
- Page 82 and 83:
1655-1672 - DE ABERRATIONE 71 probl
- Page 84 and 85:
1655-1672 - DE ABERRATIONE 73 1 ( 1
- Page 86 and 87:
1655-1672 - DE ABERRATIONE 75 Huyge
- Page 88 and 89:
1655-1672 - DE ABERRATIONE 77 Moreo
- Page 90 and 91:
1655-1672 - DE ABERRATIONE 79 carry
- Page 92 and 93:
1655-1672 - DE ABERRATIONE 81 the o
- Page 94 and 95:
1655-1672 - DE ABERRATIONE 83 specu
- Page 96 and 97:
1655-1672 - DE ABERRATIONE 85 to go
- Page 98 and 99:
1655-1672 - DE ABERRATIONE 87 Newto
- Page 100 and 101:
1655-1672 - DE ABERRATIONE 89 In hi
- Page 102 and 103:
1655-1672 - DE ABERRATIONE 91 Philo
- Page 104 and 105:
1655-1672 - DE ABERRATIONE 93 its e
- Page 106 and 107:
1655-1672 - DE ABERRATIONE 95 Newto
- Page 108 and 109:
1655-1672 - DE ABERRATIONE 97 pheno
- Page 110 and 111:
1655-1672 - DE ABERRATIONE 99 exten
- Page 112 and 113:
1655-1672 - DE ABERRATIONE 101 circ
- Page 114 and 115:
1655-1672 - DE ABERRATIONE 103 his
- Page 116 and 117:
1655-1672 - DE ABERRATIONE 105 livi
- Page 118 and 119:
Chapter 4 The 'Projet' of 1672 The
- Page 120 and 121:
THE 'PROJET' OF 1672 109 physical f
- Page 122 and 123:
THE 'PROJET' OF 1672 111 In the ‘
- Page 124 and 125:
THE 'PROJET' OF 1672 113 seventeent
- Page 126 and 127:
THE 'PROJET' OF 1672 115 truncated
- Page 128 and 129:
THE 'PROJET' OF 1672 117 mechanical
- Page 130 and 131:
THE 'PROJET' OF 1672 119 matter. In
- Page 132 and 133:
Kepler began with the understanding
- Page 134 and 135:
THE 'PROJET' OF 1672 123 True measu
- Page 136 and 137:
THE 'PROJET' OF 1672 125 The most i
- Page 138 and 139:
semicircle in M, and drop MN, cutti
- Page 140 and 141:
THE 'PROJET' OF 1672 129 apply to C
- Page 142 and 143:
THE 'PROJET' OF 1672 131 the first
- Page 144 and 145:
THE 'PROJET' OF 1672 133 analogies,
- Page 146 and 147:
THE 'PROJET' OF 1672 135 room for d
- Page 148 and 149:
THE 'PROJET' OF 1672 137 consisted
- Page 150 and 151:
THE 'PROJET' OF 1672 139 Lectiones
- Page 152 and 153:
THE 'PROJET' OF 1672 141 Figure 44
- Page 154 and 155:
THE 'PROJET' OF 1672 143 crystal is
- Page 156 and 157:
THE 'PROJET' OF 1672 145 Figure 49
- Page 158 and 159:
THE 'PROJET' OF 1672 147 the fixed
- Page 160 and 161:
THE 'PROJET' OF 1672 149 Figure 54
- Page 162 and 163:
THE 'PROJET' OF 1672 151 “I have
- Page 164 and 165:
efracted wave and thus perpendicula
- Page 166 and 167:
THE 'PROJET' OF 1672 155 unequal bo
- Page 168 and 169:
THE 'PROJET' OF 1672 157 experience
- Page 170 and 171:
Chapter 5 1677-1679 - Waves of Ligh
- Page 172 and 173:
1677-1679 -WAVES OF LIGHT 161 Amids
- Page 174 and 175:
1677-1679 -WAVES OF LIGHT 163 secon
- Page 176 and 177:
1677-1679 -WAVES OF LIGHT 165 On th
- Page 178 and 179:
1677-1679 -WAVES OF LIGHT 167 subor
- Page 180 and 181:
1677-1679 -WAVES OF LIGHT 169 some
- Page 182 and 183:
1677-1679 -WAVES OF LIGHT 171 of th
- Page 184 and 185:
1677-1679 -WAVES OF LIGHT 173 depen
- Page 186 and 187:
1677-1679 -WAVES OF LIGHT 175 his r
- Page 188 and 189:
1677-1679 -WAVES OF LIGHT 177 He be
- Page 190 and 191:
1677-1679 -WAVES OF LIGHT 179 Figur
- Page 192 and 193:
1677-1679 -WAVES OF LIGHT 181 diffe
- Page 194 and 195:
1677-1679 -WAVES OF LIGHT 183 formu
- Page 196 and 197:
1677-1679 -WAVES OF LIGHT 185 The e
- Page 198 and 199:
1677-1679 -WAVES OF LIGHT 187 Desca
- Page 200 and 201:
1677-1679 -WAVES OF LIGHT 189 may n
- Page 202 and 203:
1677-1679 -WAVES OF LIGHT 191 under
- Page 204 and 205:
1677-1679 -WAVES OF LIGHT 193 Hooke
- Page 206 and 207:
1677-1679 -WAVES OF LIGHT 195 proof
- Page 208 and 209:
1677-1679 -WAVES OF LIGHT 197 refra
- Page 210 and 211:
velocity at incidence and of the sq
- Page 212 and 213:
1677-1679 -WAVES OF LIGHT 201 If Ne
- Page 214 and 215:
1677-1679 -WAVES OF LIGHT 203 appli
- Page 216 and 217:
1677-1679 -WAVES OF LIGHT 205 some
- Page 218 and 219:
1677-1679 -WAVES OF LIGHT 207 have
- Page 220 and 221:
1677-1679 -WAVES OF LIGHT 209 shoul
- Page 222 and 223:
1677-1679 -WAVES OF LIGHT 211 Huyge
- Page 224 and 225:
Chapter 6 1690 - Traité de la Lumi
- Page 226 and 227:
1690 - TRAITÉ DE LA LUMIÈRE 215 p
- Page 228 and 229:
1690 - TRAITÉ DE LA LUMIÈRE 217 t
- Page 230 and 231:
1690 - TRAITÉ DE LA LUMIÈRE 219 A
- Page 232 and 233:
1690 - TRAITÉ DE LA LUMIÈRE 221 i
- Page 234 and 235:
1690 - TRAITÉ DE LA LUMIÈRE 223 u
- Page 236 and 237:
1690 - TRAITÉ DE LA LUMIÈRE 225
- Page 238 and 239:
1690 - TRAITÉ DE LA LUMIÈRE 227 a
- Page 240 and 241:
1690 - TRAITÉ DE LA LUMIÈRE 229 m
- Page 242 and 243:
1690 - TRAITÉ DE LA LUMIÈRE 231 m
- Page 244 and 245:
1690 - TRAITÉ DE LA LUMIÈRE 233 p
- Page 246 and 247:
1690 - TRAITÉ DE LA LUMIÈRE 235 d
- Page 248 and 249:
1690 - TRAITÉ DE LA LUMIÈRE 237 T
- Page 250 and 251:
1690 - TRAITÉ DE LA LUMIÈRE 239 s
- Page 252 and 253:
1690 - TRAITÉ DE LA LUMIÈRE 241 p
- Page 254 and 255:
1690 - TRAITÉ DE LA LUMIÈRE 243 W
- Page 256 and 257:
1690 - TRAITÉ DE LA LUMIÈRE 245 F
- Page 258 and 259:
1690 - TRAITÉ DE LA LUMIÈRE 247 o
- Page 260 and 261:
1690 - TRAITÉ DE LA LUMIÈRE 249 t
- Page 262 and 263:
1690 - TRAITÉ DE LA LUMIÈRE 251 a
- Page 264 and 265:
1690 - TRAITÉ DE LA LUMIÈRE 253 S
- Page 266 and 267:
Chapter 7 Conclusion: Lenses & Wave
- Page 268 and 269:
LENSES & WAVES 257 foundations. Bos
- Page 270 and 271:
LENSES & WAVES 259 phenomena. The c
- Page 272 and 273:
LENSES & WAVES 261 other part of ph
- Page 274 and 275:
LENSES & WAVES 263 mathematical phy
- Page 276 and 277:
List of figures Figure 1 Huygens: s
- Page 278 and 279:
Bibliography References are made by
- Page 280 and 281:
BIBLIOGRAPHY 269 Boas Hall, Marie.
- Page 282 and 283:
BIBLIOGRAPHY 271 Daumas, Maurice. S
- Page 284 and 285:
BIBLIOGRAPHY 273 Gregory, David. Dr
- Page 286 and 287:
BIBLIOGRAPHY 275 Horstmann, Frank.
- Page 288 and 289:
BIBLIOGRAPHY 277 Lohne, Johannes.
- Page 290 and 291:
BIBLIOGRAPHY 279 Newton, Isaac. The
- Page 292 and 293:
BIBLIOGRAPHY 281 Schuster, John A.
- Page 294 and 295:
BIBLIOGRAPHY 283 Uylenbroek, Petrus
- Page 296 and 297:
Index Académie Royale des Sciences
- Page 298:
160, 195, 197-201, 203, 217, 223, 2