Grundlagen der Spektrumanalyse.pdf - Ing. H. Heuermann

Grundlagen der Spektrumanalyse
Signale
Periodische Signale
Das Theorem von Fourier besagt, daß jedes beliebige im Zeitbereich periodische
Signal aus einer Summe von sinus- und cosinusförmigen Signalen
unterschiedlicher Frequenz und Amplitude gebildet werden kann. Eine solche
Summe wird als Fourier-Reihe bezeichnet. Es gilt:
x(t)
0
n = 1
n = 3
n = 5 n = 7
Harmonische
x(t)
0
Summe der Harmonischen
A 0
x(t) = +Σ A n · sin(n · ω 0 · t) +Σ B n · cos(n · ω 0 · t) (Gl. 2-4)
2
∞
n=1
∞
n=1
Die Fourier-Koeffizienten A 0 , A n und B n sind abhängig von der Kurvenform
des Signals x(t) und können wie folgt berechnet werden:
2
A 0 = ∫ x(t)dt (Gl. 2-5)
T 0
T 0
0
2
A n = ∫ x(t) · sin(n · ω 0 · t) dt (Gl. 2-6)
T 0
T 0
0
2
B n = ∫ x(t) · cos(n · ω 0 · t) dt (Gl. 2-7)
T 0
T 0
0
t
a) b)
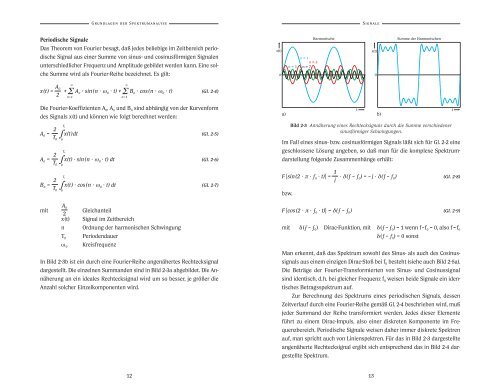
Bild 2-3 Annäherung eines Rechtecksignals durch die Summe verschiedener
sinusförmiger Schwingungen.
Im Fall eines sinus- bzw. cosinusförmigen Signals läßt sich für Gl. 2-2 eine
geschlossene Lösung angeben, so daß man für die komplexe Spektrumdarstellung
folgende Zusammenhänge erhält:
1
F {sin(2 · π · ƒ 0 · t)} = · δ(ƒ – ƒ 0 ) = – j · δ(ƒ– ƒ 0 ) (Gl. 2-8)
j
bzw.
t
mit
A 0
2
x(t)
n
T 0
ω 0
Gleichanteil
Signal im Zeitbereich
Ordnung der harmonischen Schwingung
Periodendauer
Kreisfrequenz
In Bild 2-3b ist ein durch eine Fourier-Reihe angenähertes Rechtecksignal
dargestellt. Die einzelnen Summanden sind in Bild 2-3a abgebildet. Die Annäherung
an ein ideales Rechtecksignal wird um so besser, je größer die
Anzahl solcher Einzelkomponenten wird.
F {cos(2 · π · ƒ 0 · t)} = δ(ƒ – ƒ 0 ) (Gl. 2-9)
mit δ(ƒ – ƒ 0 ) Dirac-Funktion, mit δ(ƒ– ƒ 0 ) = 1 wenn f–f 0 = 0, also f=f 0
δ(ƒ – ƒ 0 ) = 0 sonst
Man erkennt, daß das Spektrum sowohl des Sinus- als auch des Cosinussignals
aus einem einzigen Dirac-Stoß bei f 0 besteht (siehe auch Bild 2-5a).
Die Beträge der Fourier-Transformierten von Sinus- und Cosinussignal
sind identisch, d.h. bei gleicher Frequenz f 0 weisen beide Signale ein identisches
Betragsspektrum auf.
Zur Berechnung des Spektrums eines periodischen Signals, dessen
Zeitverlauf durch eine Fourier-Reihe gemäß Gl. 2-4 beschrieben wird, muß
jeder Summand der Reihe transformiert werden. Jedes dieser Elemente
führt zu einem Dirac-Impuls, also einer diskreten Komponente im Frequenzbereich.
Periodische Signale weisen daher immer diskrete Spektren
auf, man spricht auch von Linienspektren. Für das in Bild 2-3 dargestellte
angenäherte Rechtecksignal ergibt sich entsprechend das in Bild 2-4 dargestellte
Spektrum.
12
13