Processus de Lévy en Finance - Laboratoire de Probabilités et ...

124 CHAPTER 3. NUMERICAL IMPLEMENTATION
0.4
0.38
Variance gamma
Calibrated with σ=0.25
Calibrated with σ=0.2
15
True VG Levy measure
Calibrated with σ=0.25
Calibrated with σ=0.2
0.36
10
0.34
0.32
5
0.3
0.28
0.7 0.8 0.9 1 1.1 1.2 1.3 1.4
0
−0.5 0 0.5
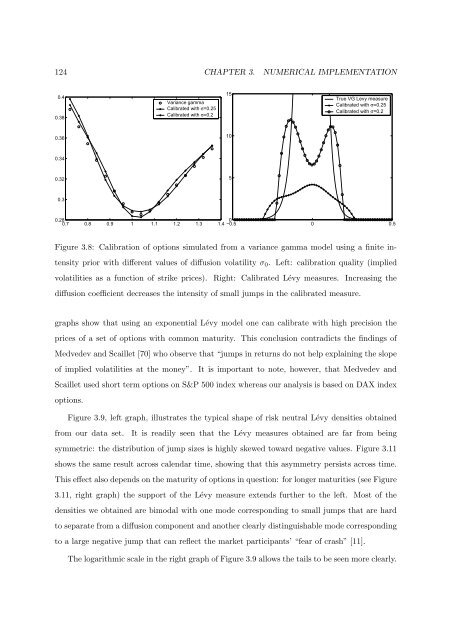
Figure 3.8: Calibration of options simulated from a variance gamma model using a finite intensity
prior with different values of diffusion volatility σ 0 . Left: calibration quality (implied
volatilities as a function of strike prices). Right: Calibrated Lévy measures. Increasing the
diffusion coefficient decreases the intensity of small jumps in the calibrated measure.
graphs show that using an exponential Lévy model one can calibrate with high precision the
prices of a set of options with common maturity. This conclusion contradicts the findings of
Medvedev and Scaillet [70] who observe that “jumps in returns do not help explaining the slope
of implied volatilities at the money”. It is important to note, however, that Medvedev and
Scaillet used short term options on S&P 500 index whereas our analysis is based on DAX index
options.
Figure 3.9, left graph, illustrates the typical shape of risk neutral Lévy densities obtained
from our data set. It is readily seen that the Lévy measures obtained are far from being
symmetric: the distribution of jump sizes is highly skewed toward negative values. Figure 3.11
shows the same result across calendar time, showing that this asymmetry persists across time.
This effect also depends on the maturity of options in question: for longer maturities (see Figure
3.11, right graph) the support of the Lévy measure extends further to the left. Most of the
densities we obtained are bimodal with one mode corresponding to small jumps that are hard
to separate from a diffusion component and another clearly distinguishable mode corresponding
to a large negative jump that can reflect the market participants’ “fear of crash” [11].
The logarithmic scale in the right graph of Figure 3.9 allows the tails to be seen more clearly.