Processus de Lévy en Finance - Laboratoire de Probabilités et ...

126 CHAPTER 3. NUMERICAL IMPLEMENTATION
5
4.5
4
3.5
11 May 2001, 8 days
11 June 2001, 4 days
11 July 2001, 9 days
Prior
4
3.5
3
11 May 2001, 36 days
11 June 2001, 39 days
11 July 2001, 37 days
Prior
3
2.5
2.5
2
2
1.5
1.5
1
1
0.5
0.5
0
−0.5 −0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4
0
−1 −0.8 −0.6 −0.4 −0.2 0 0.2
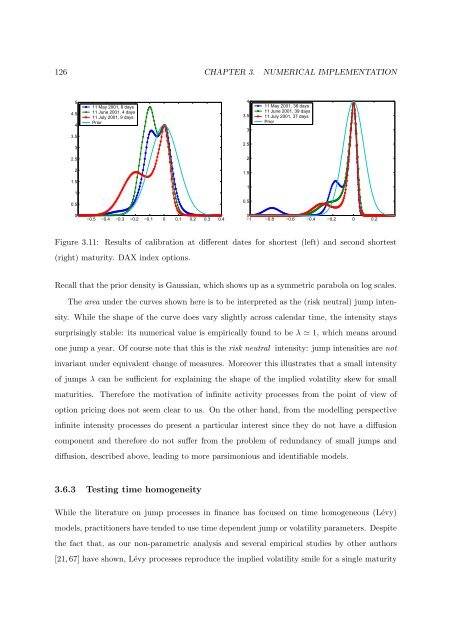
Figure 3.11: Results of calibration at different dates for shortest (left) and second shortest
(right) maturity. DAX index options.
Recall that the prior density is Gaussian, which shows up as a symmetric parabola on log scales.
The area under the curves shown here is to be interpreted as the (risk neutral) jump intensity.
While the shape of the curve does vary slightly across calendar time, the intensity stays
surprisingly stable: its numerical value is empirically found to be λ ≃ 1, which means around
one jump a year. Of course note that this is the risk neutral intensity: jump intensities are not
invariant under equivalent change of measures. Moreover this illustrates that a small intensity
of jumps λ can be sufficient for explaining the shape of the implied volatility skew for small
maturities. Therefore the motivation of infinite activity processes from the point of view of
option pricing does not seem clear to us. On the other hand, from the modelling perspective
infinite intensity processes do present a particular interest since they do not have a diffusion
component and therefore do not suffer from the problem of redundancy of small jumps and
diffusion, described above, leading to more parsimonious and identifiable models.
3.6.3 Testing time homogeneity
While the literature on jump processes in finance has focused on time homogeneous (Lévy)
models, practitioners have tended to use time dependent jump or volatility parameters. Despite
the fact that, as our non-parametric analysis and several empirical studies by other authors
[21, 67] have shown, Lévy processes reproduce the implied volatility smile for a single maturity