Guide to COST-BENEFIT ANALYSIS of investment projects - Ramiri

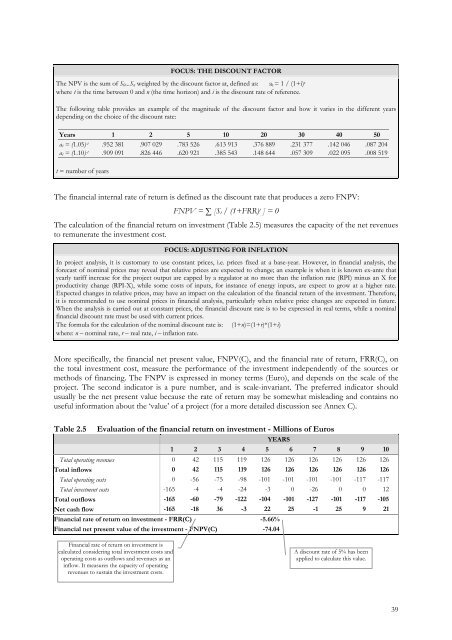
FOCUS: THE DISCOUNT FACTORThe NPV is the sum of S 0 ...S n weighted by the discount factor at, defined as: a t = 1 / (1+i) twhere t is the time between 0 and n (the time horizon) and i is the discount rate of reference.The following table provides an example of the magnitude of the discount factor and how it varies in the different yearsdepending on the choice of the discount rate:Years 1 2 5 10 20 30 40 50a t = (1.05) -t .952 381 .907 029 .783 526 .613 913 .376 889 .231 377 .142 046 .087 204a t = (1.10) -t .909 091 .826 446 .620 921 .385 543 .148 644 .057 309 .022 095 .008 519t = number of yearsThe financial internal rate of return is defined as the discount rate that produces a zero FNPV:FNPV = ∑ [S t / (1+FRR) t ] = 0The calculation of the financial return on investment (Table 2.5) measures the capacity of the net revenuesto remunerate the investment cost.FOCUS: ADJUSTING FOR INFLATIONIn project analysis, it is customary to use constant prices, i.e. prices fixed at a base-year. However, in financial analysis, theforecast of nominal prices may reveal that relative prices are expected to change; an example is when it is known ex-ante thatyearly tariff increase for the project output are capped by a regulator at no more than the inflation rate (RPI) minus an X forproductivity change (RPI-X), while some costs of inputs, for instance of energy inputs, are expect to grow at a higher rate.Expected changes in relative prices, may have an impact on the calculation of the financial return of the investment. Therefore,it is recommended to use nominal prices in financial analysis, particularly when relative price changes are expected in future.When the analysis is carried out at constant prices, the financial discount rate is to be expressed in real terms, while a nominalfinancial discount rate must be used with current prices.The formula for the calculation of the nominal discount rate is: (1+n)=(1+r)*(1+i)where: n – nominal rate, r – real rate, i – inflation rate.More specifically, the financial net present value, FNPV(C), and the financial rate of return, FRR(C), onthe total investment cost, measure the performance of the investment independently of the sources ormethods of financing. The FNPV is expressed in money terms (Euro), and depends on the scale of theproject. The second indicator is a pure number, and is scale-invariant. The preferred indicator shouldusually be the net present value because the rate of return may be somewhat misleading and contains nouseful information about the ‘value’ of a project (for a more detailed discussion see Annex C).Table 2.5 Evaluation of the financial return on investment - Millions of EurosYEARS1 2 3 4 5 6 7 8 9 10Total operating revenues 0 42 115 119 126 126 126 126 126 126Total inflows 0 42 115 119 126 126 126 126 126 126Total operating costs 0 -56 -75 -98 -101 -101 -101 -101 -117 -117Total investment costs -165 -4 -4 -24 -3 0 -26 0 0 12Total outflows -165 -60 -79 -122 -104 -101 -127 -101 -117 -105Net cash flow -165 -18 36 -3 22 25 -1 25 9 21Financial rate of return on investment - FRR(C) -5.66%Financial net present value of the investment - FNPV(C) -74.04Financial rate of return on investment iscalculated considering total investment costs andoperating costs as outflows and revenues as aninflow. It measures the capacity of operatingrevenues to sustain the investment costs.A discount rate of 5% has beenapplied to calculate this value.39