- Page 1 and 2:
PROJETO DE ALGORITMOS PARA RESOLUÇ
- Page 3 and 4:
Agradecimentos Em primeiro lugar, a
- Page 5 and 6:
Abstract of Thesis presented to COP
- Page 7 and 8:
2.5.4 Outras considerações sobre
- Page 9 and 10:
3.6 Conclusões deste capítulo . .
- Page 11 and 12:
5.13 Conclusões deste capítulo .
- Page 13 and 14:
de análise e síntese (ou projeto)
- Page 15 and 16:
de Bhaya e Kaszkurewicz. Porém, to
- Page 17 and 18:
a estabilidade do sistema. Já a me
- Page 19 and 20:
também outros algoritmos, podem se
- Page 21 and 22:
escalares convexas sujeitas a restr
- Page 23 and 24:
uma trajetória da variável x a pa
- Page 25 and 26:
e os algoritmos discretos assim des
- Page 27 and 28:
levando ao chamado sistema em malha
- Page 29 and 30:
De (2.9) e (2.3), pode-se escrever:
- Page 31 and 32:
det(D f (x)) = 0. 2) Segunda escolh
- Page 33 and 34:
existindo portanto convergência em
- Page 35 and 36:
Existe também a possibilidade de m
- Page 37 and 38:
fechada ẋ = D −1 f r que corres
- Page 39 and 40:
Observe-se também que ([41, lema 2
- Page 41 and 42:
O hessiano da função primitiva, e
- Page 43 and 44:
A partir deste gráfico podemos che
- Page 45 and 46:
1 0.8 0.6 Algoritmos de primeira or
- Page 47 and 48:
det(D f ) = 0, porém, a seguinte e
- Page 49 and 50:
Cabe destacar que Gomulka ([34]) n
- Page 51 and 52:
⎡ ⎣ − ∂f 1 ∂f 2 ∂ ∂x
- Page 53 and 54:
onde x ∗ = [0 1] T é um zero da
- Page 55 and 56:
onde k é o número de zero a ser l
- Page 57 and 58:
Observe-se que, assumindo f 2 (x)
- Page 59 and 60:
⇒ det(D f (x)) = 8a 2 x 2 1 − 8
- Page 61 and 62:
Para a constante c = 0.13, o determ
- Page 63 and 64:
dades estranhas. O algoritmo NV apl
- Page 65 and 66:
escolha do comprimento do passo α
- Page 67 and 68:
Este algoritmo coincide com a vers
- Page 69 and 70:
do vetor D T f (x k)f(x k ) seja ig
- Page 71 and 72:
Foi adotado como critério de parad
- Page 73 and 74:
0.8 0.6 0.4 Algoritmos discretos de
- Page 75 and 76:
Camelback Rosenbrock Branin x 0 it.
- Page 77 and 78:
onde ⎡ A = ⎢ ⎣ 4 4 4 4 1 1 1
- Page 79 and 80:
onde ⎡ A = ⎢ ⎣ ⎤ 10 3 17 3.
- Page 81 and 82:
DN DNV DJT DVJT DJTV N x 0 it. t[s]
- Page 83 and 84:
o hessiano da função. 2.6.3 Utili
- Page 85 and 86:
2.7.1 Função de Camelback Na fun
- Page 87 and 88:
d) Perto das fronteiras das faixas,
- Page 89 and 90:
a partir dos quais o algoritmo demo
- Page 91 and 92:
uma norma de valor elevado, as traj
- Page 93 and 94:
os pontos de comportamento similar
- Page 95 and 96:
2.7.3 Função de Branin. Constante
- Page 97 and 98:
1 0.8 0.6 0.4 0.2 x 2 0 f 2 =0 −0
- Page 99 and 100:
1 0.8 0.6 0.4 0.2 x 2 0 f 2 =0 −0
- Page 101 and 102:
Caso a função φ(x) não seja con
- Page 103 and 104:
A primeira escolha será aquela cor
- Page 105 and 106:
Ver detalhes da prova em [6, teorem
- Page 107 and 108:
sistema será chamado de steepest d
- Page 109 and 110:
4 3.5 3 2.5 2 Algoritmos contínuos
- Page 111 and 112:
2.8.2 Discretização dos algoritmo
- Page 113 and 114:
e derivando com respeito a α k :
- Page 115 and 116: tantes µ = 0 e ν = 1, então ∇
- Page 117 and 118: derivados com a metodologia CLF/LOC
- Page 119 and 120: todos os pontos iniciais testados.
- Page 121 and 122: Capítulo 3 Algoritmos de segunda o
- Page 123 and 124: A diferença dos algoritmos de prim
- Page 125 and 126: 3) Terceira escolha Planta ẋ = D
- Page 127 and 128: Resumindo, a metodologia CLF/LOC se
- Page 129 and 130: −0.6739, x 1 = −1.7737. Observe
- Page 131 and 132: equação det(D f (x)) = x 2 1 −
- Page 133 and 134: Algoritmos de segunda ordem contín
- Page 135 and 136: e derivando com respeito a α k e i
- Page 137 and 138: E substituindo em (3.18) e (3.19):
- Page 139 and 140: DC2: u 0 = −Df Tf(x 0) DC3: u 0 =
- Page 141 and 142: 3.2.3.3 Simulações dos algoritmos
- Page 143 and 144: 0.8 0.6 0.4 Algoritmos de segunda o
- Page 145 and 146: 3.3 Algoritmos de segunda ordem par
- Page 147 and 148: O autor demonstra que se φ(x) e U(
- Page 149 and 150: Planta ẋ = u Substituindo em (3.3
- Page 151 and 152: ordem, mas realizando uma convenien
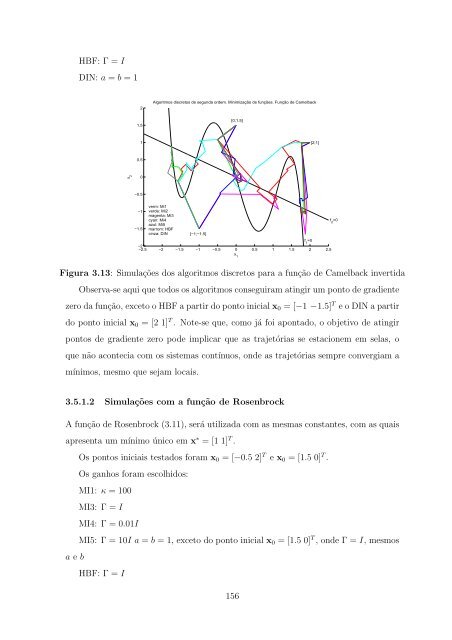
- Page 153 and 154: ordem, mas fazendo uma conveniente
- Page 155 and 156: nome planta controlador ODE MI1 ẋ
- Page 157 and 158: 2 Algoritmos contínuos de segunda
- Page 159 and 160: ultrapassa-la, para depois retornar
- Page 161 and 162: mínimo estimado γ, de maneira tal
- Page 163 and 164: E substituindo em (3.43) e (3.44):
- Page 165: nome α k β k MI1 − ∇T φ∇ 2
- Page 169 and 170: função x 0 MI1 MI2 MI3 MI4 MI5 HB
- Page 171 and 172: Capítulo 4 Algoritmo para otimiza
- Page 173 and 174: exemplo, o interessante trabalho de
- Page 175 and 176: Uma função é afim se a igualdade
- Page 177 and 178: 4.3 Descrição do problema Seguire
- Page 179 and 180: a seguinte função de energia: E(x
- Page 181 and 182: Em particular, se sobre uma superf
- Page 183 and 184: Primeiramente, sera analisado o cas
- Page 185 and 186: alternativa: V rp2 (x) = ‖x − x
- Page 187 and 188: e a derivada de Lie expressada em (
- Page 189 and 190: ∀x ∈ ∂χ : ẋ ∈ F[m](x) =
- Page 191 and 192: e de (4.47) e (4.48), concluimos: m
- Page 193 and 194: 12 Algoritmo contínuo. Trajetória
- Page 195 and 196: sendo α k o comprimento do passo.
- Page 197 and 198: comprimento do passo que, dentro de
- Page 199 and 200: Problema 1 min x 2 1 + x2 2 s.t. x
- Page 201 and 202: Exemplo 1 diversas trajetórias a p
- Page 203 and 204: 4.9 Algoritmo de gradiente projetad
- Page 205 and 206: 2 Exemplo 2 com o algoritmo de proj
- Page 207 and 208: 4.10 Conclusões deste capítulo Os
- Page 209 and 210: Capítulo 5 Algoritmo para desigual
- Page 211 and 212: se aqui um novo algoritmo contínuo
- Page 213 and 214: Teorema 5.2.8 Seja Ω um subconjunt
- Page 215 and 216: 5.3 Descrição do problema Dado um
- Page 217 and 218:
fortemente para o caso da expressã
- Page 219 and 220:
5.3.1 Função de erro A resoluçã
- Page 221 and 222:
g) ∀x ∈ χ ‖x − Pr χ [x
- Page 223 and 224:
Nos casos em que a função f(x) n
- Page 225 and 226:
Solodov e Tseng ([75]) utilizam a c
- Page 227 and 228:
Este é o terceiro problema utiliza
- Page 229 and 230:
5.5 Algoritmos para a resolução d
- Page 231 and 232:
y ∗ ∈ R m e z ∗ ∈ R p tal q
- Page 233 and 234:
⇐) Se u = u ∗ ⇒ u ∈ Ω ⇒
- Page 235 and 236:
R n , y ∈ R m +, z ∈ R p } e
- Page 237 and 238:
projeção ortogonal é trivial. 5.
- Page 239 and 240:
β k = 0. Além dessa dificuldade,
- Page 241 and 242:
de GVI do algoritmo (5.55). Dentre
- Page 243 and 244:
senta algumas vantagens com respeit
- Page 245 and 246:
Calculamos ˙V rp (x) = [ D T g (x)
- Page 247 and 248:
ẋ (ver [68]): ∀x ∈ ∂χ :
- Page 249 and 250:
5.7 Execução do algoritmo O algor
- Page 251 and 252:
O exemplo 6 é implementado com gan
- Page 253 and 254:
o operador de projeção ortogonal
- Page 255 and 256:
Otimizando o comprimento do passo s
- Page 257 and 258:
Para esses valores de α k , consid
- Page 259 and 260:
estrições violadas no ponto x k+1
- Page 261 and 262:
e este novo vetor u terá o mesmo s
- Page 263 and 264:
Observe-se que esta é a condição
- Page 265 and 266:
Neste algoritmo, chamamos de x r ao
- Page 267 and 268:
5.9 Algoritmo projetado O algoritmo
- Page 269 and 270:
2 Exemplo 2 (número de iterações
- Page 271 and 272:
Sobre o conjunto Ω é trivial calc
- Page 273 and 274:
⇒ r k+1 ≃ r k − α k [ D f (x
- Page 275 and 276:
e por LOC, derivando com respeito a
- Page 277 and 278:
2 Algoritmo 3 projetado Exemplo 1 (
- Page 279 and 280:
2 Algoritmo 3 projetado Exemplo 2 (
- Page 281 and 282:
nas bibliografias referenciadas, se
- Page 283 and 284:
possibilita análises alternativas
- Page 285 and 286:
pelo plano de fase. Apesar destes i
- Page 287 and 288:
geral de otimização convexa que n
- Page 289 and 290:
de algoritmos de continuação ou h
- Page 291 and 292:
[12] A. Bhaya and E. Kaszkurewicz.
- Page 293 and 294:
[43] S. Hedge and S. Kacera. Safegu
- Page 295 and 296:
[71] M. V. Solodov. A class of glob