Introduction to Acoustics

More documents

Recommendations

Info

Equations (22.423) are usually written in polar form A1(T1) = a1 2 eiθ1 ; A2(T1) = a2 2 eiθ2 , (22.424) where the amplitudes ai and phases θi are functions of T1. Substituting (22.424) in(22.423) yields the system that governs the slow temporal evolution of the response, with scale T1 = εt: ⎧ ∂a1 ∂T1 ⎪⎨ ∂a2 ⎪⎩ ∂T1 ∂θ1 a1 ∂T2 ∂θ2 a2 ∂T2 =−µ1a1 − β12a1a2 4ω1 sin(σ1T1 + θ2 − 2θ1) , = β12a1a2 4ω1 cos(σ1T1 + θ2 − 2θ1) , =−µ2a2 + β21a2 1 sin(σ1T1 + θ2 − 2θ1) 4ω2 + P sin(σ2T1 − θ2) , 2ω2 = β21a 2 1 4ω2 cos(σ1T1 + θ2 − 2θ1) − P cos(σ2T1 − θ2) . 2ω2 (22.425) Autonomous System and Fixed Points. Now, the system is written in autonomous form, i. e. in the form ˙X = F(X). In practice, this is achieved with the changes of variables γ1 = σ2T1 − θ2 and γ2 = σ1T1 + θ2 − 2θ1. As a consequence (22.425) becomes: ⎧ ∂a1 ∂T1 ⎪⎨ ∂a2 ⎪⎩ ∂T1 ∂γ1 ∂T2 ∂γ2 ∂T2 =−µ1a1 − β12a1a2 4ω1 sin γ2 , = σ2 − β21a2 1 cos γ2 + 4ω2a2 P cos γ1 , 2ω2a2 =−µ2a2 + β21a 2 1 4ω2 = σ1 − β12a2 2ω1 − P cos γ1 . 2ω2a2 sin γ2 + P sin γ1 , 2ω2 cos γ2 + β21a2 1 cos γ2 4ω2a2 (22.426) The fixed points correspond to the steady-state solutions, which are those of interest in the case of forced vibrations. These solutions are obtained through cancelation Structural Acoustics and Vibrations 22.7 Nonlinear Vibrations 953 of the time derivatives in (22.426), which gives: ⎧ � a1 µ1 + β12a2 � sin γ2 = 0 , 4ω1 ⎪⎨ ⎪⎩ σ2 − β21a 2 1 4ω2a2 −µ2a2 + β21a 2 1 4ω2 cos γ2 + P cos γ1 = 0 , 2ω2a2 sin γ2 + P sin γ1 = 0 , 2ω2 σ1 + β21a2 1 cos γ2 − 4ω2a2 P cos γ1 2ω2a2 − β12a2 2ω1 cos γ2 = 0 . (22.427) Imposing a1 = 0in(22.427) yields the response curve a2 of the second oscillator in the linear case (Fig. 22.29) a2 = P � 2ω2 σ 2 2 + µ2 . (22.428) 2 Stability of the Nonlinear Coupled System. Intuitively, a physically unstable system behaves in such a way that, subjected to a small departure from equilibrium, its motion will never bring it back to its initial position but will rather continue its deviation. From a mathematical point of view, the deviations from an equilibrium position for a system with multiple variables such as (22.427) are calculated from the partial derivatives of each equation with regard to all variables of the system. This leads to Amplitudes a1, a2 40 30 20 10 Mode 1 0 –50 –40 –30 Mode 1 –20 –10 0 10 Mode 2 20 30 Mode 2 40 50 Detuning σ2 Fig. 22.29 Frequency response curves of the nonlinearly coupled oscillators as a function of the external detuning parameter Part G 22.7
954 Part G Structural Acoustics and Noise Part G 22.7 the definition of the Jacobian matrix J of the system: � � ∂ f1 � � � ∂a1 � � ∂ f2 � � ∂a1 J = � � � ∂ f3 � � ∂a1 � � � ∂ f4 � ∂a1 ∂ f1 ∂γ1 ∂ f2 ∂γ1 ∂ f3 ∂γ1 ∂ f4 ∂γ1 ∂ f1 ∂a2 ∂ f2 ∂a2 ∂ f3 ∂a2 ∂ f4 ∂a2 � ∂ f1 � � ∂γ2 � � ∂ � f2 � � ∂γ2 � � ∂ f3 � . (22.429) � � ∂γ2 � � ∂ f4 � � � ∂γ2 In our case, the eigenvalues of this Jacobian are ⎧ λ1 =−µ2 + iσ2 ; ⎪⎨ λ2 =−µ2− iσ2 ; λ3 =− ⎪⎩ β12a2 sin γ2 − µ1 ; 4ω1 λ4 = β12a2 (22.430) sin γ2 . 2ω1 The system is unstable if the real part of any one of these eigenvalues is positive. In (22.430), the real parts of λ1 and λ2 are negative, because of the damping term µ2. However, calculating the product of the two other eigenvalues yields λ3λ4 =− µ1β12a2 2ω1 sin γ2 − β2 12 a2 2 8ω 2 1 sin 2 γ2 . (22.431) This product can be negative, leading to an instability, if a2 > 2ω1 � 4µ |β12| 2 1 + (σ1 + σ2) 2 . (22.432) The instability domain corresponding to (22.432) isthe shaded area in Fig. 22.29. Amplitudes and Phases of the Solution. Solutions for the nonlinear coupled system are obtained by combining (22.422) with (22.424), taking the definitions of T1, σ1, σ2 γ1 and γ2 into account. We then obtain ⎧ ⎪⎨ x10 = a1 cos(ω1t + θ1) = a1 cos ⎪⎩ � Ω 2 t − γ1+γ2 � 2 , x20 = a2 cos(ω2t + θ2) = a2 cos � � Ωt − γ1 , (22.433) where, by solving the system (22.427), the amplitudes of the oscillators are given by ⎧ a2 = ⎪⎨ 2ω1 � (σ1 + σ2) |β12| 2 + 4µ 2 1 , a1 = 2 � � − Γ1 ± P2 / � 4β2 � � 21 − Γ 2 1/2 2 , with Γ1 = 2ω1ω2 [2µ1µ2 − σ2(σ1 + σ2)] , β12β21 ⎪⎩ and Γ2 = 2ω1ω2 [2µ1σ2 − µ2(σ1 + σ2)] . β12β21 (22.434) Equation (22.433) shows that, for steady-state oscillations, the forcing frequency Ω is the same as the oscillation frequency of the second oscillator whereas, for appropriate conditions of instability, the first one oscillates with frequency Ω/2, as a result of the nonlinear coupling. Figure 22.29 shows the resonance curves of the coupled nonlinear oscillators as a function of σ2. By increasing this parameter progressively, successive phenomena occur: 1. First the resonance curve is that of the second oscillator. No subharmonics are observed as long as the amplitude remains below the instability region. 2. As the amplitude of the second oscillator reaches the instability limit given in (22.432), the first oscillator starts to oscillate. In our example, its magnitude a1 is larger than a2. Amplitudes (mm) 0.12 0.10 0.08 0.06 0.04 0.02 0 Mode 2 Mode 1 219.4 219.6 219.8 220 220.2 220.4 220.6 220.8 221.0 Excitation frequency (Hz) Fig. 22.30 Experimental response curves for two nonlinearly coupled degrees of freedom of a harmonically forced spherical shell (after Thomas et al. [22.19])
Page 2 and 3:
Springer Handbook of Acoustics
Page 4 and 5:
Springer Handbook of Acoustics Thom
Page 6 and 7:
Foreword The present handbook cover
Page 8 and 9:
List of Authors Iskander Akhatov No
Page 10 and 11:
Philippe Roux Université Joseph Fo
Page 12 and 13:
XIV Contents 3.7 Attenuation of Sou
Page 14 and 15:
XVI Contents 10 Concert Hall Acoust
Page 16 and 17:
XVIII Contents 17.8 Physical Modeli
Page 18 and 19:
XX Contents 24.5 Free-Field Microph
Page 20 and 21:
XXII List of Abbreviations K KDP po
Page 22 and 23:
Introduction 1. Introduction to Aco
Page 24 and 25:
of noise have been the subject of c
Page 26 and 27:
in order to understand how objectiv
Page 28 and 29:
A Brief 2. A Brief History of Acous
Page 30 and 31:
of 350 m/s for the speed of sound [
Page 32 and 33:
number and relative strength of its
Page 34 and 35:
To his contemporaries, Koenig was p
Page 36 and 37:
Probably the most important use of
Page 38 and 39:
piezoelectric ceramic compositions
Page 40 and 41:
surveys together [2.46]. Masking of
Page 42 and 43:
ther of computer music, since he de
Page 44 and 45:
Basic 3. Linear Basic Linear Acoust
Page 46 and 47:
M average molecular weight n unit v
Page 48 and 49:
a) b) S v.n ∆t ∆S V |v| ∆t n
Page 50 and 51:
temperature, q =−κ∇T , (3.16)
Page 52 and 53:
The equivalent density M/V is conse
Page 54 and 55:
Basic Linear Acoustics 3.3 Equation
Page 56 and 57:
Because any vector field may be dec
Page 58 and 59:
The latter and (3.84), in a manner
Page 60 and 61:
assumed to have no ambient motion,
Page 62 and 63:
Because the friction associated wit
Page 64 and 65:
3.5 Waves of Constant Frequency One
Page 66 and 67:
3.5.4 Time Averages of Products Whe
Page 68 and 69:
as well as symmetry considerations,
Page 70 and 71:
The auxiliary internal variables th
Page 72 and 73:
Then the transient at a distant pos
Page 74 and 75:
ω ′ = 0, and this is consistent
Page 76 and 77:
1.0 10 -1 10 -2 10 -3 10 -4 10 -5 A
Page 78 and 79:
This yields the interpretation that
Page 80 and 81:
direction of propagation when a pla
Page 82 and 83:
so the time-averaged incident energ
Page 84 and 85:
Although the simple result of (3.31
Page 86 and 87:
ut, also in keeping with the linear
Page 88 and 89:
equation, the two differential equa
Page 90 and 91:
Rodrigues relation, one has �1
Page 92 and 93:
for the derivative.) In the asympto
Page 94 and 95:
The differential scattering cross s
Page 96 and 97:
elow) is F(t) = (2c) 1/2 �t −
Page 98 and 99:
0.5 0 -0.5 -1.0 -1.5 0 Y0(η) (π/2
Page 100 and 101:
is the Wronskian for the Bessel and
Page 102 and 103:
The function qS is termed the sourc
Page 104 and 105:
The appropriate identification for
Page 106 and 107:
where jℓ is the spherical Bessel
Page 108 and 109:
this subtlety taken into account, o
Page 110 and 111:
U(x) Basic Linear Acoustics 3.15 Wa
Page 112 and 113:
is ordinarily valid. With these ass
Page 114 and 115:
along rays. These can be regarded a
Page 116 and 117:
A(x0) x0 A(x) Fig. 3.53 Sketch of a
Page 118 and 119:
possible, and one where neither the
Page 120 and 121:
which is independent of the z-coord
Page 122 and 123:
[3.108], and Carslaw [3.109]. In th
Page 124 and 125:
where C(X)andS(X) are the Fresnel i
Page 126 and 127:
Fig. 3.60 Characteristic diffractio
Page 128 and 129:
of elastic solids, Trans. Camb. Phi
Page 130 and 131:
3.101 J.B. Keller: Geometrical acou
Page 132 and 133:
114 Part A Propagation of Sound Par
Page 134 and 135:
Page 136 and 137:
Page 138 and 139:
Page 140 and 141:
Page 142 and 143:
Page 144 and 145:
Page 146 and 147:
Page 148 and 149:
Page 150 and 151:
Page 152 and 153:
Page 154 and 155:
Page 156 and 157:
Page 158 and 159:
Page 160 and 161:
Page 162 and 163:
Page 164 and 165:
Page 166 and 167:
Underwater 5. Underwater Acoustics
Page 168 and 169:
5.1 Ocean Acoustic Environment The
Page 170 and 171:
Long-Range Propagation Paths Figure
Page 172 and 173:
tal direction, there is no loss ass
Page 174 and 175:
equivalent circuit, as shown in Fig
Page 176 and 177:
Attenuation á (dB/km) 1000 100 10
Page 178 and 179:
5.2.5 Ambient Noise There are essen
Page 180 and 181:
ubble natural acoustic resonance ω
Page 182 and 183:
a bubbly medium (and for the simple
Page 184 and 185:
As discussed, because detection inv
Page 186 and 187:
(1/A)∇ 2 A ≪ K 2 )sothat(5.34)
Page 188 and 189:
water, where the deep sound channel
Page 190 and 191:
egion in the form p(r, z) = ψ(r, z
Page 192 and 193:
5.4.6 Propagation and Transmission
Page 194 and 195:
tegration interval. The source puls
Page 196 and 197:
5.6 SONAR Array Processing Signal p
Page 198 and 199:
former output is: �∞ b(θ,t) =
Page 200 and 201:
Fig. 5.37 Angle-versus-time represe
Page 202 and 203:
5.7 Active SONAR Processing Depth M
Page 204 and 205:
a factor when there is a reverberan
Page 206 and 207:
depth measurements that correspond
Page 208 and 209:
along the cross-shelf track taken b
Page 210 and 211:
time as a result of multiple paths,
Page 212 and 213:
technique is very sensitive, and ex
Page 214 and 215:
Fig. 5.57a,b Typical echogram obtai
Page 216 and 217:
Frequency (Hz) 150 100 50 0 0 a) b)
Page 218 and 219:
out. These data allow for study of
Page 220 and 221:
5.59 G. Raleigh, J.M. Cioffi: Spati
Page 222 and 223:
Physical 6. Physical Acou Acoustics
Page 224 and 225:
where I is the intensity of the sou
Page 226 and 227:
Wave velocity The wall exerts a dow
Page 228 and 229:
destructively interfered with one a
Page 230 and 231:
or: � � p2 � rms SPL = 10 log
Page 232 and 233:
6.1.4 Wave Propagation in Solids Si
Page 234 and 235:
where c is again the wave speed and
Page 236 and 237:
measured. Some resonances are cause
Page 238 and 239:
as 50 µmto5µm through one oscilla
Page 240 and 241:
the number of false positives and m
Page 242 and 243:
with the small mass), and frequency
Page 244 and 245:
Laser Lens 1 Circular aperture Fig.
Page 246 and 247:
Ground ring Insulator Sample Resist
Page 248 and 249:
Energy ratio 1.0 0.8 0.6 0.4 Calcul
Page 250 and 251:
terms. In this equation γ is the r
Page 252 and 253:
directly. The nonlinearity paramete
Page 254 and 255:
Thermoacoust 7. Thermoacoustics The
Page 256 and 257:
Table 7.1 The acoustic-electric ana
Page 258 and 259:
walls of the pores. (Positive G ind
Page 260 and 261:
a) b) c) C reso d) δtherm e) p 0 U
Page 262 and 263:
a) b) UA,l c) d) E 0 Q A Q A TA TA
Page 264 and 265:
tor. This eliminates the need to le
Page 266 and 267:
to this consumption of acoustic pow
Page 268 and 269:
The traditional Stirling refrigerat
Page 270 and 271:
Washington 1986) pp. 550-554, Softw
Page 272 and 273:
258 Part B Physical and Nonlinear A
Page 274 and 275:
Page 276 and 277:
Page 278 and 279:
Page 280 and 281:
Page 282 and 283:
Page 284 and 285:
Page 286 and 287:
Page 288 and 289:
Page 290 and 291:
Page 292 and 293:
Page 294 and 295:
Page 296 and 297:
Page 298 and 299:
Page 300 and 301:
Page 302 and 303:
Page 304 and 305:
Page 306 and 307:
Page 308 and 309:
Page 310 and 311:
Page 312 and 313:
Acoustics 9. Acoustics in Halls for
Page 314 and 315:
parameters, so we can assist in bui
Page 316 and 317:
weeks or even years is less reliabl
Page 318 and 319:
9.3.1 Reverberation Time Reverberan
Page 320 and 321:
selected). A distance different fro
Page 322 and 323:
ing sound, as will naturally be exp
Page 324 and 325:
of the sound fields. Consequently,
Page 326 and 327:
e derived from interrupted noise de
Page 328 and 329:
Acoustics in Halls for Speech and M
Page 330 and 331:
espectively, can be calculated from
Page 332 and 333:
ated by the architects. However, on
Page 334 and 335:
of C and G. However, as all the ind
Page 336 and 337:
F b d F n I S Fb Fn S d F n/F b d/d
Page 338 and 339:
HS S èn ã d0 P0 rn Position of ey
Page 340 and 341:
Time T (s) 2.5 2 1.5 1 5 10 15 Acou
Page 342 and 343:
floor can be tilted to reduce volum
Page 344 and 345:
ÄLcurv (dB) 10 8 6 4 2 0 -2 -4 -6
Page 346 and 347:
Page 348 and 349:
Page 350 and 351:
Page 352 and 353:
Seating capacity 2662 1 915 + 324 2
Page 354 and 355:
Page 356 and 357:
4 3 2 1 Acoustics in Halls for Spee
Page 358 and 359:
cially in auditoria with T values l
Page 360 and 361:
esonance (AR)andmultichannel reverb
Page 362 and 363:
Concert 10. Concert Hall Acoustics
Page 364 and 365:
Concert Hall Acoustics Based on Sub
Page 366 and 367:
0 0 Concert Hall Acoustics Based on
Page 368 and 369:
mately by Concert Hall Acoustics Ba
Page 370 and 371:
Page 372 and 373:
10.1.5 Specialization of Cerebral H
Page 374 and 375:
The other (n − 1) bits indicated
Page 376 and 377:
As for the conflicting requirements
Page 378 and 379:
have mainly been concerned with tem
Page 380 and 381:
a) c) S S -4.3 -2.8 -2.0 -3.5 -3dB
Page 382 and 383:
Page 384 and 385:
Page 386 and 387:
Page 388 and 389:
Page 390 and 391:
Page 392 and 393:
Page 394 and 395:
Page 396 and 397:
a model of the auditory-brain syste
Page 398 and 399:
Building 11. Building Acou Acoustic
Page 400 and 401:
Pressure Maximum Minimum 0 D Distan
Page 402 and 403:
Table 11.1 Absorption coefficients
Page 404 and 405:
Absorption coefficient α 1 0 Frequ
Page 406 and 407:
is of key importance in rooms where
Page 408 and 409:
Table 11.4 Transmission loss and ST
Page 410 and 411:
TL of wall - (TL of door, window or
Page 412 and 413:
Table 11.7 Generalized noise reduct
Page 414 and 415:
Masking sound pressure level (dB) 5
Page 416 and 417:
As for the room criterion (RC) meth
Page 418 and 419:
11.5 Noise Control Methods for Buil
Page 420 and 421:
Neoprene pads (30 durometer) with a
Page 422 and 423:
Concrete Caulk around perimeter Vib
Page 424 and 425:
Trim board to conceal gap (fasten o
Page 426 and 427:
Gypsum board partition (as schedule
Page 428 and 429:
Double-layer ribbed or waffle neopr
Page 430 and 431:
11.6 Acoustical Privacy in Building
Page 432 and 433:
Table 11.9 AI,SIIandPIforopenplanof
Page 434 and 435:
Electronic sound masking in plenum
Page 436 and 437:
E 1179 Standard Specification for S
Page 438 and 439:
430 Part D Hearing and Signal Proce
Page 440 and 441:
Page 442 and 443:
Page 444 and 445:
Page 446 and 447:
Page 448 and 449:
Page 450 and 451:
Page 452 and 453:
Page 454 and 455:
Page 456 and 457:
Page 458 and 459:
Page 460 and 461:
Page 462 and 463:
Page 464 and 465:
Page 466 and 467:
Psychoacoust 13. Psychoacoustics Ps
Page 468 and 469:
Absolute threshold (dB SPL) 100 90
Page 470 and 471:
the signal. By using this off-cente
Page 472 and 473:
is as a crude indicator of the exci
Page 474 and 475:
Relative response (dB) 100 90 80 70
Page 476 and 477:
In a variation of this procedure, t
Page 478 and 479:
Level of matching noise (dB) 100 90
Page 480 and 481:
13.4 Temporal Processing in the Aud
Page 482 and 483:
Most models include an initial stag
Page 484 and 485:
The components were either uniforml
Page 486 and 487:
(Frequency DL)/ERBN 0.2 0.1 0.05 0.
Page 488 and 489:
elaborate place models have been pr
Page 490 and 491:
13.6 Timbre Perception 13.6.1 Time-
Page 492 and 493:
the duplex theory of sound localiza
Page 494 and 495:
harmonic (by shifting the frequency
Page 496 and 497:
sive. While some studies have been
Page 498 and 499:
sentences (see Fig. 13.20). They va
Page 500 and 501:
components is usually only perceive
Page 502 and 503:
References 13.1 ISO 389-7: Acoustic
Page 504 and 505:
13.74 D. Ronken: Monaural detection
Page 506 and 507:
asymmetric function, J. Acoust. Soc
Page 508 and 509:
13.211 J. Vliegen, A.J. Oxenham: Se
Page 510 and 511:
Page 512 and 513:
Page 514 and 515:
Page 516 and 517:
Page 518 and 519:
Page 520 and 521:
Page 522 and 523:
Page 524 and 525:
Page 526 and 527:
Page 528 and 529:
Page 530 and 531:
Page 532 and 533:
Page 534 and 535:
Page 536 and 537:
Page 538 and 539:
534 Part E Music, Speech, Electroac
Page 540 and 541:
Page 542 and 543:
Page 544 and 545:
Page 546 and 547:
Page 548 and 549:
Page 550 and 551:
Page 552 and 553:
Page 554 and 555:
Page 556 and 557:
Page 558 and 559:
Page 560 and 561:
Page 562 and 563:
Page 564 and 565:
Page 566 and 567:
Page 568 and 569:
Page 570 and 571:
Page 572 and 573:
Page 574 and 575:
Page 576 and 577:
Page 578 and 579:
Page 580 and 581:
Page 582 and 583:
Page 584 and 585:
Page 586 and 587:
Page 588 and 589:
Page 590 and 591:
Page 592 and 593:
Page 594 and 595:
Page 596 and 597:
Page 598 and 599:
Page 600 and 601:
Page 602 and 603:
Page 604 and 605:
Page 606 and 607:
Page 608 and 609:
Page 610 and 611:
Page 612 and 613:
Page 614 and 615:
Page 616 and 617:
Page 618 and 619:
Page 620 and 621:
Page 622 and 623:
Page 624 and 625:
Page 626 and 627:
Page 628 and 629:
Page 630 and 631:
Page 632 and 633:
Page 634 and 635:
Page 636 and 637:
Page 638 and 639:
Page 640 and 641:
Page 642 and 643:
Page 644 and 645:
Page 646 and 647:
Page 648 and 649:
Page 650 and 651:
Page 652 and 653:
Page 654 and 655:
Page 656 and 657:
Page 658 and 659:
Page 660 and 661:
Page 662 and 663:
Page 664 and 665:
Page 666 and 667:
Page 668 and 669:
Page 670 and 671:
Page 672 and 673:
The 16. The Human Human Voice in Sp
Page 674 and 675:
uation, the effect of gravity is in
Page 676 and 677:
piratory muscles (the internal inte
Page 678 and 679:
Mean Ps (cm H2O) 50 40 30 20 10 0 D
Page 680 and 681:
Glottal flow Closed Opening Open Cl
Page 682 and 683:
Transglottal airflow (l/s) 0.4 0.2
Page 684 and 685:
Mean spectrum level (dB) -30 -40 -5
Page 686 and 687:
20 10 0 -10 -20 -30 -40 -50 0 i y u
Page 688 and 689:
Mean level (dB) 0 -10 -20 -30 -40 1
Page 690 and 691:
This topic was addressed by Ladefog
Page 692 and 693:
Fig. 16.29 Acoustic consequences of
Page 694 and 695:
Bass i e u Alto Tenor o ε œ æ Th
Page 696 and 697:
100 80 60 40 20 0 -20 100 80 60 40
Page 698 and 699:
tours for [� ]and[Ù ] sampled at
Page 700 and 701:
Rapp [16.100] asked three native sp
Page 702 and 703:
Utterance command T0 T3 Accent comm
Page 704 and 705:
The # symbol indicates the possibil
Page 706 and 707:
Second formant frequency (Hz) 2500
Page 708 and 709:
tional rather than absolute (à la
Page 710 and 711:
16.7 P. Ladefoged, M.H. Draper, D.
Page 712 and 713:
esonance imaging: Vowels, J. Acoust
Page 714 and 715:
16.139 A. Eriksson: Aspects of Swed
Page 716 and 717:
Computer 17. Computer Mu Music This
Page 718 and 719:
Quantum step Amplitude Quantization
Page 720 and 721:
Some might notice that linear inter
Page 722 and 723:
pers, textbooks, patents, etc. Furt
Page 724 and 725:
0:00.0 0.5 0 Computer Music 17.3 Ad
Page 726 and 727:
(0,0) (0,1) (1,1) (0,2) (1,2) (0,3)
Page 728 and 729:
synthesizing vocoder. The main diff
Page 730 and 731:
x(n) + z -1 z -1 Scattering junctio
Page 732 and 733:
230 Hz FOF 1100 Hz FOF 1700 Hz FOF
Page 734 and 735:
0 y + - Computer Music 17.8 Physica
Page 736 and 737:
-1 (1-ß )×length Velocity + Veloc
Page 738 and 739:
0 -30 (dB) -60 0 1.5 3 4.5 (kHz) Fi
Page 740 and 741:
17.10 Composition The history of co
Page 742 and 743:
and variance of the features can be
Page 744 and 745:
17.20 J.L. Kelly Jr., C.C. Lochbaum
Page 746 and 747:
Audio 18. Audio and Electroacoustic
Page 748 and 749:
Alexander Graham Bell filed his pat
Page 750 and 751:
on magnetic stripes. A common arran
Page 752 and 753:
60 40 20 0 SPL-sound pressure level
Page 754 and 755:
Interaural intensity difference (dB
Page 756 and 757:
with equalization, without incurrin
Page 758 and 759:
Fig. 18.8 Sine wave with crossover
Page 760 and 761:
18.3.8 Dynamic Range Dynamic range
Page 762 and 763:
Directly actuated type Diaphragm ty
Page 764 and 765:
effective pickup pattern of the arr
Page 766 and 767:
attempts to apply complementary com
Page 768 and 769:
Most of the issues relating to spea
Page 770 and 771:
nificant design considerations. At
Page 772 and 773:
Some appreciation of the performanc
Page 774 and 775:
pre-digital reverberators were elec
Page 776 and 777:
and ‘s’ in English text - may b
Page 778 and 779:
content of rest of the signal spect
Page 780 and 781:
cross the head, in opposite directi
Page 782 and 783:
18.2 J. Sterne: The Audible Past (D
Page 784 and 785:
18.71 T. Sporer: Creating, assessin
Page 786 and 787:
786 Part F Biological and Medical A
Page 788 and 789:
Page 790 and 791:
Page 792 and 793:
Page 794 and 795:
Page 796 and 797:
Page 798 and 799:
Page 800 and 801:
Page 802 and 803:
Page 804 and 805:
Page 806 and 807:
Page 808 and 809:
Page 810 and 811:
Page 812 and 813:
Page 814 and 815:
Page 816 and 817:
Page 818 and 819:
Page 820 and 821:
Page 822 and 823:
Page 824 and 825:
Page 826 and 827:
Page 828 and 829:
Page 830 and 831:
Page 832 and 833:
Page 834 and 835:
Page 836 and 837:
Page 838 and 839:
Medical 21. Medical Acous Acoustics
Page 840 and 841:
21.1 Introduction to Medical Acoust
Page 842 and 843:
Auscultation location Right & left
Page 844 and 845:
portance. The Strouhal number has b
Page 846 and 847:
Fig. 21.3 Phono-cardiograph transdu
Page 848 and 849:
Amplitude 8 6 4 2 0 -2 -4 -6 Displa
Page 850 and 851:
λ1 = c1 / fus θ1 λ2 = c2 / fus
Page 852 and 853:
lood flow can be resolved if the si
Page 854 and 855:
vided in the image thickness direct
Page 856 and 857:
not as predicted, because the wave
Page 858 and 859:
Fig. 21.18a,b Quadrature Doppler de
Page 860 and 861:
a) b) c) 100 0 V mV 10 0 a = 13 a =
Page 862 and 863:
Ultrasound contact gel Position enc
Page 864 and 865:
a) 10 cm b) c) 10 cm Fig. 21.32a-c
Page 866 and 867:
a) Pin B Pin A Ultrasound line b) M
Page 868 and 869:
Organ Patient Ultrasound transducer
Page 870 and 871:
systems cannot tell the difference
Page 872 and 873:
40 µm can be resolved. For a 10 kH
Page 874 and 875:
a) b) c) d) Medical Acoustics 21.4
Page 876 and 877:
Fig. 21.54 Doppler spectral wavefor
Page 878 and 879:
10 20 30 10 20 30 Pre-exercise B-mo
Page 880 and 881:
Vibrations in a punctured artery De
Page 882 and 883:
the veins and diffuse into the inte
Page 884 and 885:
21.5.3 Agitated Saline and Patent F
Page 886 and 887:
transported by those cells and/or r
Page 888 and 889:
1 0.8 0.6 0.4 0.2 0 Relative power
Page 890 and 891:
High intensity focused ultrasound h
Page 892 and 893:
a) b) c) Fig. 21.74a-c B-mode imagi
Page 894 and 895:
provided simple metrics for the lik
Page 896 and 897:
thickness of the carotid arteries,
Page 898 and 899:
Structural 22. Structural Acoustics
Page 900 and 901: Structural Acoustics and Vibrations
Page 902 and 903: Magnitude (arb. units) 1.4 1.2 1.0
Page 904 and 905: This does not include the case wher
Page 906 and 907: the mass matrix is taken to be cons
Page 908 and 909: Magnitude (dB) -10 -30 -50 0 1 2 3
Page 910 and 911: where D(ω) = ω 4 − 2iω 3�
Page 912 and 913: form y(x, t) = � Φn(x)qn(t) . (2
Page 914 and 915: first to solve the wave equation (2
Page 916 and 917: 5 3 1 -1 -3 -5 0 1 2 3 4 5 6 7 8 9
Page 918 and 919: conditions at each end) are necessa
Page 920 and 921: from which we can derive through (2
Page 922 and 923: In this case, the eigenfrequencies
Page 924 and 925: of radiation modes and their link w
Page 926 and 927: Finally, the displacement is ˜ξ(x
Page 928 and 929: notes the value of this eigenmode a
Page 930 and 931: Pm = ˙Q H [Rs + Ra] ˙Q , (22.262)
Page 932 and 933: where and Ra = 2ζaω0 M Z(s) = zL
Page 934 and 935: Radiated Power. The mean acoustic p
Page 936 and 937: (22.318) can be written ξ(x, y, t)
Page 938 and 939: Denoting the eigenfrequencies and e
Page 940 and 941: Magnitude (arb. units) 3 2 1 0 -1 -
Page 942 and 943: for any real symmetric tensor Xij.
Page 944 and 945: F(N) 1 0.5 0 -0.5 -1 -1 -0.8 -0.6 -
Page 946 and 947: whose solution is θ1 = A cos ωτ.
Page 948 and 949: 4.5 3.5 2.5 1.5 A 0.5 0 0.5 1.0 1.5
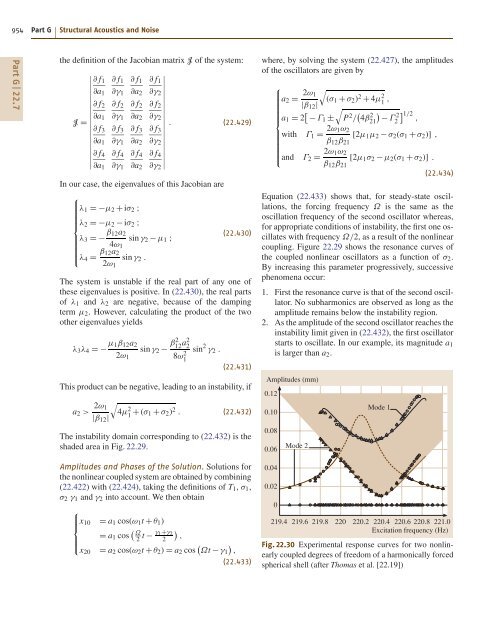
Page 952 and 953: 3. As the amplitude reaches the top
Page 954 and 955: Shallow Spherical Shells and Plates
Page 956 and 957: 22.20 L. Cremer, M. Heckl: Structur
Page 958 and 959: Noise Noise is discussed in terms o
Page 960 and 961: where the overbars represent time a
Page 962 and 963: Typical outdoor setting A-weighted
Page 964 and 965: 90 dB(A)” is widely used, and imp
Page 966 and 967: Microphone, amplifier and A/D conve
Page 968 and 969: When each segment of the measuremen
Page 970 and 971: found from � LW = Lp + 10 log A +
Page 972 and 973: surement method is the ultimate use
Page 974 and 975: An intensity analyzer is more compl
Page 976 and 977: 23.2.5 Criteria for Noise Emissions
Page 978 and 979: Table 23.5 Table of limit values fr
Page 980 and 981: a) Air flows freely to rotor Weak t
Page 982 and 983: Static efficiency normalized to its
Page 984 and 985: ful applications. Good results are
Page 986 and 987: Table 23.8 Crossover speeds for var
Page 988 and 989: Reduction of airplane engine noise
Page 990 and 991: A variety of materials are used to
Page 992 and 993: ∆LF (dB) 0 -10 -20 α -30 0.05 0.
Page 994 and 995: Absorption coefficient 1.0 0.8 0.6
Page 996 and 997: high enough that there is little so
Page 998 and 999: 23.4.4 Criteria for Noise Immission
Page 1000 and 1001:
Table 23.10 (cont.) Some features o
Page 1002 and 1003:
Noise 23.4 Noise and the Receiver 1
Page 1004 and 1005:
view of administrative procedures r
Page 1006 and 1007:
provides recommendations for a foll
Page 1008 and 1009:
sound power levels of noise sources
Page 1010 and 1011:
23.68 ISO: ISO 9296:1988 Acoustics
Page 1012 and 1013:
in impedance tubes - Part 2: Transf
Page 1014 and 1015:
23.194 Commission of the European C
Page 1016 and 1017:
1022 Part H Engineering Acoustics P
Page 1018 and 1019:
Page 1020 and 1021:
Page 1022 and 1023:
Page 1024 and 1025:
Page 1026 and 1027:
Page 1028 and 1029:
Page 1030 and 1031:
Page 1032 and 1033:
Page 1034 and 1035:
Page 1036 and 1037:
Page 1038 and 1039:
Page 1040 and 1041:
Page 1042 and 1043:
Page 1044 and 1045:
Page 1046 and 1047:
Sound 25. Intens Sound Intensity So
Page 1048 and 1049:
Under such conditions the intensity
Page 1050 and 1051:
a) Pressure and particle velocity 0
Page 1052 and 1053:
τ is a dummy time variable. The ca
Page 1054 and 1055:
Error in intensity (dB) 5 0 -5 -10
Page 1056 and 1057:
8 7 6 5 4 3 2 1 0 -1 -2 -3 Error du
Page 1058 and 1059:
crophones are calibrated with a pis
Page 1060 and 1061:
Sound power level (dB re 1 pW) 72 7
Page 1062 and 1063:
it is relatively straightforward si
Page 1064 and 1065:
intensity normal to the source. Thi
Page 1066 and 1067:
25.9 W. Maysenhölder: The reactive
Page 1068 and 1069:
25.77 ISO: ISO 11205 Acoustics - No
Page 1070 and 1071:
Page 1072 and 1073:
Page 1074 and 1075:
Page 1076 and 1077:
Page 1078 and 1079:
Page 1080 and 1081:
Page 1082 and 1083:
Page 1084 and 1085:
Page 1086 and 1087:
Page 1088 and 1089:
Page 1090 and 1091:
Page 1092 and 1093:
Optical 27. Optical Methods Metho f
Page 1094 and 1095:
course also present in ordinary hol
Page 1096 and 1097:
Optical Methods for Acoustics and V
Page 1098 and 1099:
Page 1100 and 1101:
Page 1102 and 1103:
50 100 150 200 250 300 350 400 450
Page 1104 and 1105:
a) b) Optical Methods for Acoustics
Page 1106 and 1107:
nm 1000 0 -1000 150 y (mm) 100 50 O
Page 1108 and 1109:
Page 1110 and 1111:
Page 1112 and 1113:
Laser Optical Methods for Acoustics
Page 1114 and 1115:
References 27.1 E.F.F. Chladni: Die
Page 1116 and 1117:
27.75 E.-L.Johansson, L. Benckert,
Page 1118 and 1119:
Page 1120 and 1121:
Page 1122 and 1123:
Page 1124 and 1125:
Page 1126 and 1127:
Page 1128 and 1129:
Page 1130 and 1131:
About the Authors Iskander Akhatov
Page 1132 and 1133:
Neville H. Fletcher Chapter F.19 Au
Page 1134 and 1135:
Brian C. J. Moore Chapter D.13 Univ
Page 1136 and 1137:
Detailed Contents List of Abbreviat
Page 1138 and 1139:
3.8.3 Acoustic Power ..............
Page 1140 and 1141:
4.8.3 Typical Speed of Sound Profil
Page 1142 and 1143:
7.3 Engines .......................
Page 1144 and 1145:
10 Concert Hall Acoustics Based on
Page 1146 and 1147:
13.4 Temporal Processing in the Aud
Page 1148 and 1149:
15.2.5 String-Bridge-Body Coupling
Page 1150 and 1151:
19.6 Birds ........................
Page 1152 and 1153:
22.4.5 Combinations of Elementary S
Page 1154 and 1155:
24.8 Overall View on Microphone Cal
Page 1156 and 1157:
Subject Index 3 dB bandwidth 463 A
Page 1158 and 1159:
British Medical Ultrasound Society
Page 1160 and 1161:
electric circuit analogues - acoust
Page 1162 and 1163:
hyperspeech 703 hypospeech 703 I IA
Page 1164 and 1165:
- participation factors 909 - stiff
Page 1166 and 1167:
- musical instruments 541 - musical
Page 1168 and 1169:
- nonlinear vibrations 957 - plate
Page 1170 and 1171:
subjective preference theory 353 su
show all

Introduction to Acoustics

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?