Vorlesungsskript Finanzmathematik I

3.6 Optimales Stoppen und Amerikanische Optionen 50
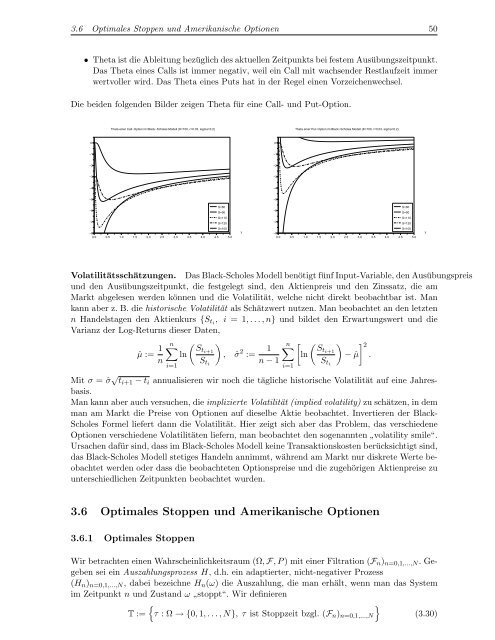
• Theta ist die Ableitung bezüglich des aktuellen Zeitpunkts bei festem Ausübungszeitpunkt.
Das Theta eines Calls ist immer negativ, weil ein Call mit wachsender Restlaufzeit immer
wertvoller wird. Das Theta eines Puts hat in der Regel einen Vorzeichenwechsel.
Die beiden folgenden Bilder zeigen Theta für eine Call- und Put-Option.
Theta einer Call−Option im Black−Scholes Modell (K=100, r=0.03, sigma=0.2)
Theta einer Put−Option im Black−Scholes Modell (K=100, r=0.03, sigma=0.2)
0
0
−1
−1
−2
−2
−3
−3
−4
−4
−5
−5
−6
S=80
S=90
−6
S=80
S=90
−7
S=110
S=120
−7
S=110
S=120
S=100
−8
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
T
S=100
−8
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
T
Volatilitätsschätzungen. Das Black-Scholes Modell benötigt fünf Input-Variable, den Ausübungspreis
und den Ausübungszeitpunkt, die festgelegt sind, den Aktienpreis und den Zinssatz, die am
Markt abgelesen werden können und die Volatilität, welche nicht direkt beobachtbar ist. Man
kann aber z. B. die historische Volatilität als Schätzwert nutzen. Man beobachtet an den letzten
n Handelstagen den Aktienkurs {S ti , i = 1, . . . , n} und bildet den Erwartungswert und die
Varianz der Log-Returns dieser Daten,
ˆµ := 1 n∑
( )
Sti+1
ln , ˆσ 2 := 1 n∑
[ ( ) 2 Sti+1
ln − ˆµ]
.
n S ti n − 1 S ti
i=1
Mit σ = ˆσ √ t i+1 − t i annualisieren wir noch die tägliche historische Volatilität auf eine Jahresbasis.
Man kann aber auch versuchen, die implizierte Volatilität (implied volatility) zu schätzen, in dem
man am Markt die Preise von Optionen auf dieselbe Aktie beobachtet. Invertieren der Black-
Scholes Formel liefert dann die Volatilität. Hier zeigt sich aber das Problem, das verschiedene
Optionen verschiedene Volatilitäten liefern, man beobachtet den sogenannten ”
volatility smile“.
Ursachen dafür sind, dass im Black-Scholes Modell keine Transaktionskosten berücksichtigt sind,
das Black-Scholes Modell stetiges Handeln annimmt, während am Markt nur diskrete Werte beobachtet
werden oder dass die beobachteten Optionspreise und die zugehörigen Aktienpreise zu
unterschiedlichen Zeitpunkten beobachtet wurden.
i=1
3.6 Optimales Stoppen und Amerikanische Optionen
3.6.1 Optimales Stoppen
Wir betrachten einen Wahrscheinlichkeitsraum (Ω, F, P ) mit einer Filtration (F n ) n=0,1,...,N . Gegeben
sei ein Auszahlungsprozess H, d.h. ein adaptierter, nicht-negativer Prozess
(H n ) n=0,1,...,N , dabei bezeichne H n (ω) die Auszahlung, die man erhält, wenn man das System
im Zeitpunkt n und Zustand ω stoppt“. Wir definieren
”
}
T :=
{τ : Ω → {0, 1, . . . , N}, τ ist Stoppzeit bzgl. (F n ) n=0,1,...,N (3.30)