Einführung in die Maß- und Integrationstheorie

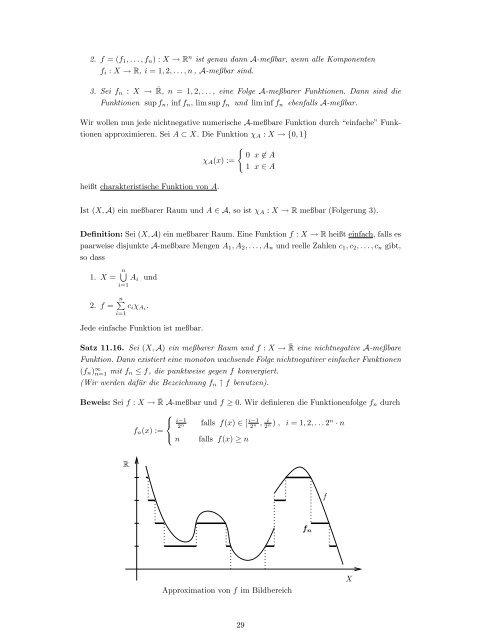
2. f = (f 1 , . . . , f n ) : X → R n ist genau dann A-meßbar, wenn alle Komponentenf i : X → R, i = 1, 2, . . . , n , A-meßbar sind.3. Sei f n : X → ¯R, n = 1, 2, . . . , eine Folge A-meßbarer Funktionen. Dann sind dieFunktionen sup f n , inf f n , lim sup f n und lim inf f n ebenfalls A-meßbar.Wir wollen nun jede nichtnegative numerische A-meßbare Funktion durch “einfache” Funktionenapproximieren. Sei A ⊂ X. Die Funktion χ A : X → {0, 1}χ A (x) :=heißt charakteristische Funktion von A.{0 x ∉ A1 x ∈ AIst (X, A) ein meßbarer Raum und A ∈ A, so ist χ A : X → R meßbar (Folgerung 3).Definition: Sei (X, A) ein meßbarer Raum. Eine Funktion f : X → R heißt einfach, falls espaarweise disjunkte A-meßbare Mengen A 1 , A 2 , . . . , A n und reelle Zahlen c 1 , c 2 , . . . , c n gibt,so dass1. X = n ⋃A ii=1und∑2. f = n c i χ Ai .i=1Jede einfache Funktion ist meßbar.Satz 11.16. Sei (X, A) ein meßbarer Raum und f : X → ¯R eine nichtnegative A-meßbareFunktion. Dann existiert eine monoton wachsende Folge nichtnegativer einfacher Funktionen(f n ) ∞ n=1 mit f n ≤ f, die punktweise gegen f konvergiert.(Wir werden dafür die Bezeichnung f n ↑ f benutzen).Beweis: Sei f : X → ¯R A-meßbar und f ≥ 0. Wir definieren die Funktionenfolge f n durch⎧⎨ i−12falls f(x) ∈ [ i−1 if n (x) :=n 2, n 2) , i = 1, 2, . . . 2 n · nn⎩ n falls f(x) ≥ nRff nApproximation von f im BildbereichX29