Agilent Spectrum Analysis Basics - Agilent Technologies

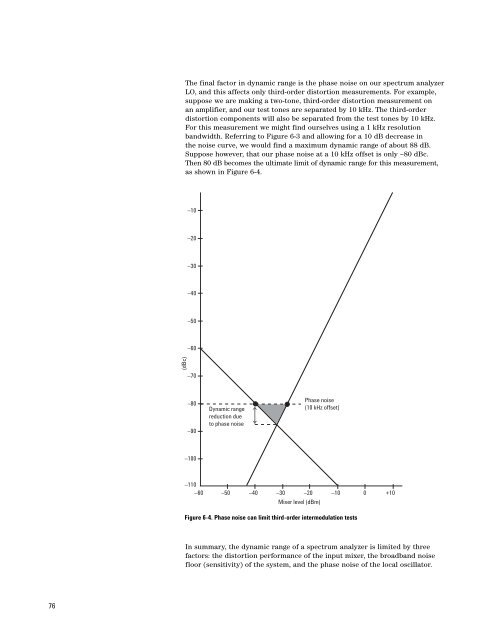
The final factor in dynamic range is the phase noise on our spectrum analyzer
LO, and this affects only third-order distortion measurements. For example,
suppose we are making a two-tone, third-order distortion measurement on
an amplifier, and our test tones are separated by 10 kHz. The third-order
distortion components will also be separated from the test tones by 10 kHz.
For this measurement we might find ourselves using a 1 kHz resolution
bandwidth. Referring to Figure 6-3 and allowing for a 10 dB decrease in
the noise curve, we would find a maximum dynamic range of about 88 dB.
Suppose however, that our phase noise at a 10 kHz offset is only –80 dBc.
Then 80 dB becomes the ultimate limit of dynamic range for this measurement,
as shown in Figure 6-4.
–10
–20
–30
–40
–50
(dBc)
–60
–70
–80
–90
Dynamic range
reduction due
to phase noise
Phase noise
(10 kHz offset)
–100
–110
–60 –50 –40 –30 –20 –10 0 +10
Mixer level (dBm)
Figure 6-4. Phase noise can limit third-order intermodulation tests
In summary, the dynamic range of a spectrum analyzer is limited by three
factors: the distortion performance of the input mixer, the broadband noise
floor (sensitivity) of the system, and the phase noise of the local oscillator.
76