Agilent Spectrum Analysis Basics - Agilent Technologies

Looking at these expressions, we see that the amplitude of the lower
distortion component (2ω 1 – ω 2 ) varies as the square of V 1 and linearly
with V 2 . On the other side, the amplitude of the upper distortion component
(2ω 2 – ω 1 ) varies linearly with V 1 and as the square of V 2 . However,
depending on the signal frequencies and separation, the preselector may
not attenuate the two fundamental tones equally.
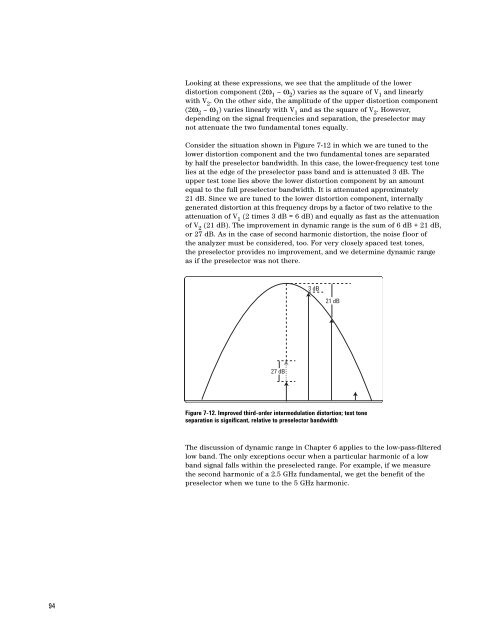
Consider the situation shown in Figure 7-12 in which we are tuned to the
lower distortion component and the two fundamental tones are separated
by half the preselector bandwidth. In this case, the lower-frequency test tone
lies at the edge of the preselector pass band and is attenuated 3 dB. The
upper test tone lies above the lower distortion component by an amount
equal to the full preselector bandwidth. It is attenuated approximately
21 dB. Since we are tuned to the lower distortion component, internally
generated distortion at this frequency drops by a factor of two relative to the
attenuation of V 1 (2 times 3 dB = 6 dB) and equally as fast as the attenuation
of V 2 (21 dB). The improvement in dynamic range is the sum of 6 dB + 21 dB,
or 27 dB. As in the case of second harmonic distortion, the noise floor of
the analyzer must be considered, too. For very closely spaced test tones,
the preselector provides no improvement, and we determine dynamic range
as if the preselector was not there.
3 dB
21 dB
27 dB
Figure 7-12. Improved third-order intermodulation distortion; test tone
separation is significant, relative to preselector bandwidth
The discussion of dynamic range in Chapter 6 applies to the low-pass-filtered
low band. The only exceptions occur when a particular harmonic of a low
band signal falls within the preselected range. For example, if we measure
the second harmonic of a 2.5 GHz fundamental, we get the benefit of the
preselector when we tune to the 5 GHz harmonic.
94