Agilent Spectrum Analysis Basics - Agilent Technologies

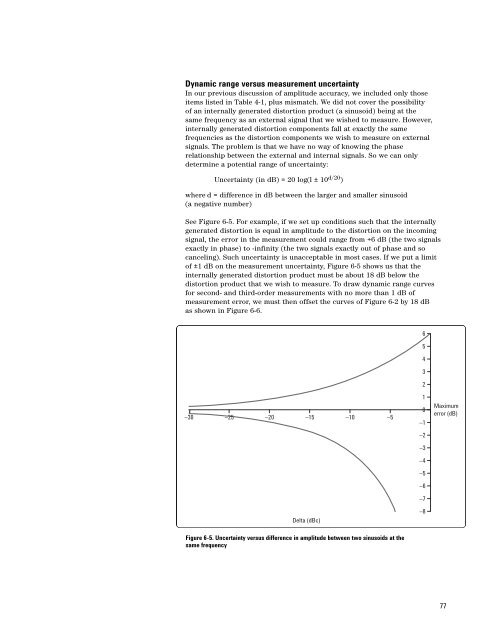
Dynamic range versus measurement uncertainty
In our previous discussion of amplitude accuracy, we included only those
items listed in Table 4-1, plus mismatch. We did not cover the possibility
of an internally generated distortion product (a sinusoid) being at the
same frequency as an external signal that we wished to measure. However,
internally generated distortion components fall at exactly the same
frequencies as the distortion components we wish to measure on external
signals. The problem is that we have no way of knowing the phase
relationship between the external and internal signals. So we can only
determine a potential range of uncertainty:
Uncertainty (in dB) = 20 log(l ± 10 d/20 )
where d = difference in dB between the larger and smaller sinusoid
(a negative number)
See Figure 6-5. For example, if we set up conditions such that the internally
generated distortion is equal in amplitude to the distortion on the incoming
signal, the error in the measurement could range from +6 dB (the two signals
exactly in phase) to -infinity (the two signals exactly out of phase and so
canceling). Such uncertainty is unacceptable in most cases. If we put a limit
of ±1 dB on the measurement uncertainty, Figure 6-5 shows us that the
internally generated distortion product must be about 18 dB below the
distortion product that we wish to measure. To draw dynamic range curves
for second- and third-order measurements with no more than 1 dB of
measurement error, we must then offset the curves of Figure 6-2 by 18 dB
as shown in Figure 6-6.
6
5
4
3
2
–30 –25
–20 –15 –10 –5
Delta (dBc)
1
0
–1
–2
–3
–4
–5
–6
–7
–8
Maximum
error (dB)
Figure 6-5. Uncertainty versus difference in amplitude between two sinusoids at the
same frequency
77