Agilent Spectrum Analysis Basics - Agilent Technologies

In Chapter 2, we used a mathematical approach to conclude that we needed
a low-pass filter. As we shall see, things become more complex in the situation
here, so we shall use a graphical approach as an easier method to see what is
happening. The low band is the simpler case, so we shall start with that. In
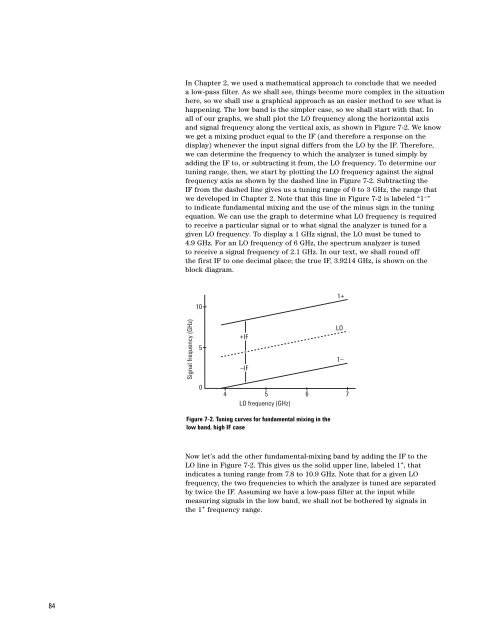
all of our graphs, we shall plot the LO frequency along the horizontal axis
and signal frequency along the vertical axis, as shown in Figure 7-2. We know
we get a mixing product equal to the IF (and therefore a response on the
display) whenever the input signal differs from the LO by the IF. Therefore,
we can determine the frequency to which the analyzer is tuned simply by
adding the IF to, or subtracting it from, the LO frequency. To determine our
tuning range, then, we start by plotting the LO frequency against the signal
frequency axis as shown by the dashed line in Figure 7-2. Subtracting the
IF from the dashed line gives us a tuning range of 0 to 3 GHz, the range that
we developed in Chapter 2. Note that this line in Figure 7-2 is labeled “1 – ”
to indicate fundamental mixing and the use of the minus sign in the tuning
equation. We can use the graph to determine what LO frequency is required
to receive a particular signal or to what signal the analyzer is tuned for a
given LO frequency. To display a 1 GHz signal, the LO must be tuned to
4.9 GHz. For an LO frequency of 6 GHz, the spectrum analyzer is tuned
to receive a signal frequency of 2.1 GHz. In our text, we shall round off
the first IF to one decimal place; the true IF, 3.9214 GHz, is shown on the
block diagram.
1+
10
Signal frequency (GHz)
5
+IF
–IF
LO
1–
0
4
5
LO frequency (GHz)
6
7
Figure 7-2. Tuning curves for fundamental mixing in the
low band, high IF case
Now let’s add the other fundamental-mixing band by adding the IF to the
LO line in Figure 7-2. This gives us the solid upper line, labeled 1 + , that
indicates a tuning range from 7.8 to 10.9 GHz. Note that for a given LO
frequency, the two frequencies to which the analyzer is tuned are separated
by twice the IF. Assuming we have a low-pass filter at the input while
measuring signals in the low band, we shall not be bothered by signals in
the 1 + frequency range.
84