Einführung in die Integralrechnung mit ... - idmthemen

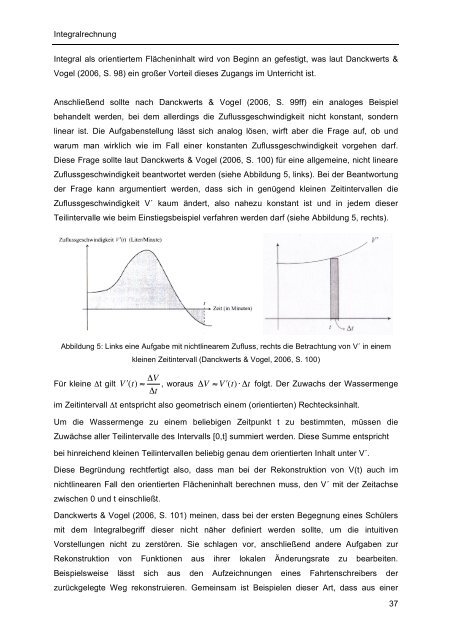
IntegralrechnungIntegral als orientiertem Flächeninhalt wird von Beginn an gefestigt, was laut Danckwerts &Vogel (2006, S. 98) ein großer Vorteil dieses Zugangs im Unterricht ist.Anschließend sollte nach Danckwerts & Vogel (2006, S. 99ff) ein analoges Beispielbehandelt werden, bei dem allerdings die Zuflussgeschwindigkeit nicht konstant, sondernlinear ist. Die Aufgabenstellung lässt sich analog lösen, wirft aber die Frage auf, ob undwarum man wirklich wie im Fall einer konstanten Zuflussgeschwindigkeit vorgehen darf.Diese Frage sollte laut Danckwerts & Vogel (2006, S. 100) für eine allgemeine, nicht lineareZuflussgeschwindigkeit beantwortet werden (siehe Abbildung 5, links). Bei der Beantwortungder Frage kann argumentiert werden, dass sich in genügend kleinen Zeitintervallen dieZuflussgeschwindigkeit V´ kaum ändert, also nahezu konstant ist und in jedem dieserTeilintervalle wie beim Einstiegsbeispiel verfahren werden darf (siehe Abbildung 5, rechts).Abbildung 5: Links eine Aufgabe mit nichtlinearem Zufluss, rechts die Betrachtung von V´ in einemFür kleine !t giltkleinen Zeitintervall (Danckwerts & Vogel, 2006, S. 100)V "(t) # $V$t , woraus"V # V $(t) % "t folgt. Der Zuwachs der Wassermengeim Zeitintervall !t entspricht also geometrisch einem (orientierten) Rechtecksinhalt.Um die Wassermenge zu ! einem beliebigen Zeitpunkt t zu bestimmten, müssen die!Zuwächse aller Teilintervalle des Intervalls [0,t] summiert werden. Diese Summe entsprichtbei hinreichend kleinen Teilintervallen beliebig genau dem orientierten Inhalt unter V´.Diese Begründung rechtfertigt also, dass man bei der Rekonstruktion von V(t) auch imnichtlinearen Fall den orientierten Flächeninhalt berechnen muss, den V´ mit der Zeitachsezwischen 0 und t einschließt.Danckwerts & Vogel (2006, S. 101) meinen, dass bei der ersten Begegnung eines Schülersmit dem Integralbegriff dieser nicht näher definiert werden sollte, um die intuitivenVorstellungen nicht zu zerstören. Sie schlagen vor, anschließend andere Aufgaben zurRekonstruktion von Funktionen aus ihrer lokalen Änderungsrate zu bearbeiten.Beispielsweise lässt sich aus den Aufzeichnungen eines Fahrtenschreibers derzurückgelegte Weg rekonstruieren. Gemeinsam ist Beispielen dieser Art, dass aus einer37