- Page 1 and 2: Preface It has been more than a dec
- Page 3 and 4: viii Contributors Björn P. Meij (5
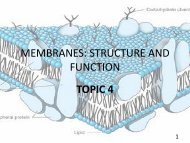
- Page 5 and 6: 2 Chapter | 1 Concepts of Normality
- Page 7 and 8: 4 Chapter | 1 Concepts of Normality
- Page 9 and 10: 6 Chapter | 1 Concepts of Normality
- Page 11 and 12: 8 Chapter | 1 Concepts of Normality
- Page 13 and 14: 10 Chapter | 1 Concepts of Normalit
- Page 15 and 16: 12 Chapter | 1 Concepts of Normalit
- Page 17 and 18: 14 Chapter | 1 Concepts of Normalit
- Page 19 and 20: 16 Chapter | 1 Concepts of Normalit
- Page 21 and 22: 18 Chapter | 1 Concepts of Normalit
- Page 23 and 24: 20 Chapter | 1 Concepts of Normalit
- Page 25: 22 Chapter | 1 Concepts of Normalit
- Page 29 and 30: Chapter 2 Comparative Medical Genet
- Page 31 and 32: I. Introduction 29 Green Red Green
- Page 33 and 34: I. Introduction 31 A1 genetic map d
- Page 35 and 36: I. Introduction 33 of genomes of va
- Page 38 and 39: 36 Chapter | 2 Comparative Medical
- Page 40 and 41: 38 Chapter | 2 Comparative Medical
- Page 42 and 43: 40 Chapter | 2 Comparative Medical
- Page 44 and 45: 42 Chapter | 2 Comparative Medical
- Page 46 and 47: 44 Chapter | 2 Comparative Medical
- Page 48 and 49: 46 Chapter | 3 Carbohydrate Metabol
- Page 50 and 51: 48 Chapter | 3 Carbohydrate Metabol
- Page 52 and 53: 50 Chapter | 3 Carbohydrate Metabol
- Page 54 and 55: 52 Chapter | 3 Carbohydrate Metabol
- Page 56 and 57: 54 Chapter | 3 Carbohydrate Metabol
- Page 58 and 59: 56 Chapter | 3 Carbohydrate Metabol
- Page 60 and 61: 58 Chapter | 3 Carbohydrate Metabol
- Page 62 and 63: 60 Chapter | 3 Carbohydrate Metabol
- Page 64 and 65: 62 Chapter | 3 Carbohydrate Metabol
- Page 66 and 67: 64 Chapter | 3 Carbohydrate Metabol
- Page 68 and 69: 66 Chapter | 3 Carbohydrate Metabol
- Page 71 and 72: IX. Disorders of Carbohydrate Metab
- Page 73 and 74: IX. Disorders of Carbohydrate Metab
- Page 75 and 76: IX. Disorders of Carbohydrate Metab
- Page 77 and 78:
X. Disorders of Ruminants Associate
- Page 79 and 80:
X. Disorders of Ruminants Associate
- Page 81 and 82:
References 79 Kaneko , J. J. , Luic
- Page 83 and 84:
Chapter 4 Lipids and Ketones Michae
- Page 85 and 86:
II. Long Chain Fatty Acids 83 FIGUR
- Page 87 and 88:
II. Long Chain Fatty Acids 85 Plasm
- Page 89 and 90:
IV. Phospholipids 87 The regulation
- Page 91 and 92:
V. Cholesterol 89 V. CHOLESTEROL A.
- Page 93 and 94:
VI. Lipoproteins 91 TABLE 4-1 Compo
- Page 95 and 96:
VI. Lipoproteins 93 TABLE 4-2 Apoli
- Page 98 and 99:
96 Chapter | 4 Lipids and Ketones B
- Page 100 and 101:
98 Chapter | 4 Lipids and Ketones
- Page 102 and 103:
100 Chapter | 4 Lipids and Ketones
- Page 104 and 105:
102 Chapter | 4 Lipids and Ketones
- Page 106 and 107:
104 Chapter | 4 Lipids and Ketones
- Page 108 and 109:
106 Chapter | 4 Lipids and Ketones
- Page 110 and 111:
108 Chapter | 4 Lipids and Ketones
- Page 112 and 113:
110 Chapter | 4 Lipids and Ketones
- Page 114 and 115:
112 Chapter | 4 Lipids and Ketones
- Page 116 and 117:
114 Chapter | 4 Lipids and Ketones
- Page 118 and 119:
Chapter 5 Proteins, Proteomics, and
- Page 120 and 121:
III. Metabolism of Proteins 119 C .
- Page 122 and 123:
IV. Plasma Proteins 121 NH 4 HCO
- Page 124 and 125:
V. Methodology 123 molecule. The gl
- Page 126 and 127:
V. Methodology 125 has occurred wil
- Page 128 and 129:
V. Methodology 127 Although attempt
- Page 130 and 131:
V. Methodology 129 kD 94 67 43 2 2
- Page 132 and 133:
V. Methodology 131 D . Specific Pro
- Page 134 and 135:
VI. Normal Plasma and Serum Protein
- Page 136 and 137:
VI. Normal Plasma and Serum Protein
- Page 138 and 139:
VI. Normal Plasma and Serum Protein
- Page 140 and 141:
VI. Normal Plasma and Serum Protein
- Page 142 and 143:
VI. Normal Plasma and Serum Protein
- Page 144 and 145:
VII. Interpretation of Serum Protei
- Page 146 and 147:
VII. Interpretation of Serum Protei
- Page 148 and 149:
VII. Interpretation of Serum Protei
- Page 150 and 151:
References 149 Andersson , M. , Ste
- Page 152 and 153:
References 151 response of haptoglo
- Page 154 and 155:
References 153 dogs with metastasiz
- Page 156 and 157:
References 155 Watson , T. D. G. (
- Page 158:
158 Chapter | 6 Clinical Veterinary
- Page 163 and 164:
V. Methods for Evaluation of the Im
- Page 165 and 166:
V. Methods for Evaluation of the Im
- Page 167 and 168:
V. Methods for Evaluation of the Im
- Page 169:
VI. Laboratory Diagnosis of Disease
- Page 173 and 174:
Chapter 7 The Erythrocyte: Physiolo
- Page 175 and 176:
II. Hematopoiesis 175 progenitor ce
- Page 177 and 178:
III. Developing Erythroid Cells 177
- Page 179 and 180:
III. Developing Erythroid Cells 179
- Page 181 and 182:
III. Developing Erythroid Cells 181
- Page 183 and 184:
III. Developing Erythroid Cells 183
- Page 185 and 186:
IV. Mature RBC 185 immune-mediated
- Page 187 and 188:
IV. Mature RBC 187 TABLE 7-3 Erythr
- Page 189 and 190:
IV. Mature RBC 189 TABLE 7.5 Erythr
- Page 191 and 192:
IV. Mature RBC 191 Echinocyte forma
- Page 193 and 194:
IV. Mature RBC 193 Pig RBC isoantig
- Page 195 and 196:
IV. Mature RBC 195 occurs in chicke
- Page 197 and 198:
IV. Mature RBC 197 inorganic phosph
- Page 199 and 200:
IV. Mature RBC 199 (a) FIGURE 7-6 T
- Page 201 and 202:
IV. Mature RBC 201 RBC 2,3DPG incre
- Page 203 and 204:
IV. Mature RBC 203 mechanisms would
- Page 205 and 206:
IV. Mature RBC 205 released during
- Page 207 and 208:
IV. Mature RBC 207 reduced by ascor
- Page 209 and 210:
V. Determinants of RBC Survival 209
- Page 211 and 212:
V. Determinants of RBC Survival 211
- Page 213 and 214:
VI. Inherited Disorders of RBCs 213
- Page 215 and 216:
VI. Inherited Disorders of RBCs 215
- Page 217 and 218:
VI. Inherited Disorders of RBCs 217
- Page 219 and 220:
described in people. They include a
- Page 221 and 222:
References 221 Boas , F. E. , Forma
- Page 223 and 224:
References 223 Della Rovere , F. ,
- Page 225 and 226:
References 225 Gedde , M. M. , Davi
- Page 227 and 228:
References 227 phosphofructokinase-
- Page 229 and 230:
References 229 Knight , A. P. , Las
- Page 231 and 232:
References 231 Martinovich , D. , a
- Page 233 and 234:
References 233 Pearson , W. , Boerm
- Page 235 and 236:
References 235 Shadduck , R. K. ( 1
- Page 237 and 238:
References 237 Tennant , B. , Dill
- Page 239 and 240:
References 239 Williams , D. M. , L
- Page 241 and 242:
Chapter 8 Porphyrins and the Porphy
- Page 243 and 244:
II. Porphyrins 243 two vinyl groups
- Page 245 and 246:
II. Porphyrins 245 TABLE 8-2 Nomenc
- Page 247 and 248:
IV. Porphyrias 247 6. Uroporphyrins
- Page 249 and 250:
IV. Porphyrias 249 i . Urine It is
- Page 251 and 252:
IV. Porphyrias 251 to localize the
- Page 253 and 254:
IV. Porphyrias 253 FIGURE 8-6 Metab
- Page 255 and 256:
IV. Porphyrias 255 estrogens. The d
- Page 257 and 258:
References 257 and hexachlorobenzen
- Page 259 and 260:
Chapter 9 Iron Metabolism and Its D
- Page 261 and 262:
II. Iron Distribution 261 plasma of
- Page 263 and 264:
IV. Plasma Iron Transport 263 pathw
- Page 265 and 266:
VI. Iron Metabolism in Cells 265 of
- Page 267 and 268:
VI. Iron Metabolism in Cells 267 in
- Page 269 and 270:
VII. Tests for Evaluating Iron Meta
- Page 271 and 272:
VII. Tests for Evaluating Iron Meta
- Page 273 and 274:
VIII. Disorders of Iron Metabolism
- Page 275 and 276:
VIII. Disorders of Iron Metabolism
- Page 277 and 278:
VIII. Disorders of Iron Metabolism
- Page 279 and 280:
References 279 ( Norrdin et al ., 2
- Page 281 and 282:
References 281 Fresco , R. ( 1981 )
- Page 283 and 284:
References 283 Moore , C. V. , Duba
- Page 285 and 286:
References 285 Weiden , P. L. , Hac
- Page 287 and 288:
288 Chapter | 10 Hemostasis TABLE 1
- Page 289 and 290:
290 Chapter | 10 Hemostasis TABLE 1
- Page 291 and 292:
292 Chapter | 10 Hemostasis The pro
- Page 293 and 294:
294 Chapter | 10 Hemostasis exhibit
- Page 295 and 296:
296 Chapter | 10 Hemostasis TABLE 1
- Page 297 and 298:
298 Chapter | 10 Hemostasis that is
- Page 299 and 300:
300 Chapter | 10 Hemostasis TABLE 1
- Page 301 and 302:
302 Chapter | 10 Hemostasis However
- Page 303 and 304:
304 Chapter | 10 Hemostasis 2. Comp
- Page 305 and 306:
306 Chapter | 10 Hemostasis is a re
- Page 307 and 308:
308 Chapter | 10 Hemostasis 2. Asse
- Page 309 and 310:
310 Chapter | 10 Hemostasis necessi
- Page 311 and 312:
312 Chapter | 10 Hemostasis disease
- Page 313 and 314:
314 Chapter | 10 Hemostasis concent
- Page 315 and 316:
316 Chapter | 10 Hemostasis the rol
- Page 317 and 318:
318 Chapter | 10 Hemostasis proport
- Page 319 and 320:
320 Chapter | 10 Hemostasis a consi
- Page 321 and 322:
322 Chapter | 10 Hemostasis Bakhtia
- Page 323 and 324:
324 Chapter | 10 Hemostasis Dowd ,
- Page 325 and 326:
326 Chapter | 10 Hemostasis Kier ,
- Page 327 and 328:
328 Chapter | 10 Hemostasis Nielsen
- Page 329 and 330:
330 Chapter | 10 Hemostasis Tablin
- Page 331 and 332:
332 Chapter | 11 Neutrophil Functio
- Page 333 and 334:
334 Chapter | 11 Neutrophil Functio
- Page 335 and 336:
336 Chapter | 11 Neutrophil Functio
- Page 337 and 338:
338 Chapter | 11 Neutrophil Functio
- Page 339 and 340:
340 Chapter | 11 Neutrophil Functio
- Page 341 and 342:
342 Chapter | 11 Neutrophil Functio
- Page 343 and 344:
344 Chapter | 11 Neutrophil Functio
- Page 345 and 346:
346 Chapter | 11 Neutrophil Functio
- Page 347 and 348:
348 Chapter | 11 Neutrophil Functio
- Page 349 and 350:
350 Chapter | 11 Neutrophil Functio
- Page 351 and 352:
352 Chapter | 12 Diagnostic Enzymol
- Page 353 and 354:
354 Chapter | 12 Diagnostic Enzymol
- Page 355 and 356:
356 Chapter | 12 Diagnostic Enzymol
- Page 357 and 358:
358 Chapter | 12 Diagnostic Enzymol
- Page 359 and 360:
360 Chapter | 12 Diagnostic Enzymol
- Page 361 and 362:
362 Chapter | 12 Diagnostic Enzymol
- Page 363 and 364:
364 Chapter | 12 Diagnostic Enzymol
- Page 365 and 366:
366 Chapter | 12 Diagnostic Enzymol
- Page 367 and 368:
368 Chapter | 12 Diagnostic Enzymol
- Page 369 and 370:
370 Chapter | 12 Diagnostic Enzymol
- Page 371 and 372:
372 Chapter | 12 Diagnostic Enzymol
- Page 373 and 374:
374 Chapter | 12 Diagnostic Enzymol
- Page 375 and 376:
376 Chapter | 12 Diagnostic Enzymol
- Page 377 and 378:
378 Chapter | 12 Diagnostic Enzymol
- Page 379 and 380:
380 Chapter | 13 Hepatic Function L
- Page 381 and 382:
382 Chapter | 13 Hepatic Function e
- Page 383 and 384:
384 Chapter | 13 Hepatic Function p
- Page 385 and 386:
386 Chapter | 13 Hepatic Function m
- Page 387 and 388:
388 Chapter | 13 Hepatic Function s
- Page 389 and 390:
390 Chapter | 13 Hepatic Function f
- Page 391 and 392:
392 Chapter | 13 Hepatic Function T
- Page 393 and 394:
394 Chapter | 13 Hepatic Function 2
- Page 395 and 396:
396 Chapter | 13 Hepatic Function u
- Page 397 and 398:
398 Chapter | 13 Hepatic Function 2
- Page 399 and 400:
400 Chapter | 13 Hepatic Function c
- Page 401 and 402:
402 Chapter | 13 Hepatic Function F
- Page 403 and 404:
404 Chapter | 13 Hepatic Function A
- Page 405 and 406:
406 Chapter | 13 Hepatic Function E
- Page 407 and 408:
408 Chapter | 13 Hepatic Function K
- Page 409 and 410:
410 Chapter | 13 Hepatic Function R
- Page 411 and 412:
412 Chapter | 13 Hepatic Function W
- Page 413 and 414:
414 Chapter | 14 Gastrointestinal F
- Page 415 and 416:
416 Chapter | 14 Gastrointestinal F
- Page 417 and 418:
418 Chapter | 14 Gastrointestinal F
- Page 419 and 420:
420 Chapter | 14 Gastrointestinal F
- Page 421 and 422:
422 Chapter | 14 Gastrointestinal F
- Page 423 and 424:
424 Chapter | 14 Gastrointestinal F
- Page 425 and 426:
426 Chapter | 14 Gastrointestinal F
- Page 427 and 428:
428 Chapter | 14 Gastrointestinal F
- Page 429 and 430:
430 Chapter | 14 Gastrointestinal F
- Page 431 and 432:
432 Chapter | 14 Gastrointestinal F
- Page 433 and 434:
434 Chapter | 14 Gastrointestinal F
- Page 435 and 436:
436 Chapter | 14 Gastrointestinal F
- Page 437 and 438:
438 Chapter | 14 Gastrointestinal F
- Page 439 and 440:
440 Chapter | 14 Gastrointestinal F
- Page 441 and 442:
442 Chapter | 14 Gastrointestinal F
- Page 443 and 444:
444 Chapter | 14 Gastrointestinal F
- Page 445 and 446:
446 Chapter | 14 Gastrointestinal F
- Page 447 and 448:
448 Chapter | 14 Gastrointestinal F
- Page 449 and 450:
450 Chapter | 14 Gastrointestinal F
- Page 451 and 452:
452 Chapter | 14 Gastrointestinal F
- Page 453 and 454:
454 Chapter | 14 Gastrointestinal F
- Page 455 and 456:
456 Chapter | 14 Gastrointestinal F
- Page 457 and 458:
Chapter 15 Skeletal Muscle Function
- Page 459 and 460:
II. Specialization of the Sarcolemm
- Page 461 and 462:
II. Specialization of the Sarcolemm
- Page 463 and 464:
III. Heterogeneity of Skeletal Musc
- Page 465 and 466:
III. Heterogeneity of Skeletal Musc
- Page 467 and 468:
V. Exercise and Adaptations to Trai
- Page 469 and 470:
VI. Diagnostic Laboratory Methods f
- Page 471 and 472:
VI. Diagnostic Laboratory Methods f
- Page 473 and 474:
IX. Selected Neuromuscular Disorder
- Page 475 and 476:
IX. Selected Neuromuscular Disorder
- Page 477 and 478:
References 479 and, recently, there
- Page 479 and 480:
References 481 Engel , A. G. ( 2004
- Page 481 and 482:
References 483 Paciello , O. , Maio
- Page 483 and 484:
Chapter 16 Kidney Function and Dama
- Page 485 and 486:
II. Kidney Morphology and Function
- Page 487 and 488:
II. Kidney Morphology and Function
- Page 489 and 490:
III. Tests of Kidney Function 491 (
- Page 491 and 492:
III. Tests of Kidney Function 493 T
- Page 493 and 494:
III. Tests of Kidney Function 495 B
- Page 495 and 496:
6 5 4 3 2 1 0 Dog Cat Equine Cattle
- Page 497 and 498:
III. Tests of Kidney Function 499 d
- Page 499 and 500:
IV. Tests of Kidney Damage 501 1000
- Page 501 and 502:
IV. Tests of Kidney Damage 503 and
- Page 503 and 504:
IV. Tests of Kidney Damage 505 Enzy
- Page 505 and 506:
V. Biochemical Changes in Kidney Di
- Page 507 and 508:
V. Biochemical Changes in Kidney Di
- Page 509 and 510:
References 511 were reported to occ
- Page 511 and 512:
References 513 Bovee , K. C. ( 1969
- Page 513 and 514:
References 515 Deguchi , E. , and A
- Page 515 and 516:
References 517 Fleming , S. A. , Hu
- Page 517 and 518:
References 519 Harvey , D. G. ( 197
- Page 519 and 520:
References 521 Kühl , S. , Mischke
- Page 521 and 522:
References 523 creatinine measureme
- Page 523 and 524:
References 525 Reusch , C. , Vochez
- Page 525 and 526:
References 527 Terry , R. , Hawkins
- Page 527 and 528:
Chapter 17 Fluid, Electrolyte, and
- Page 530 and 531:
532 Chapter | 17 Fluid, Electrolyte
- Page 534 and 535:
536 Chapter | 17 Fluid, Electrolyte
- Page 536 and 537:
538 Chapter | 17 Fluid, Electrolyte
- Page 538 and 539:
540 Chapter | 17 Fluid, Electrolyte
- Page 540 and 541:
542 Chapter | 17 Fluid, Electrolyte
- Page 542 and 543:
544 Chapter | 17 Fluid, Electrolyte
- Page 544 and 545:
546 Chapter | 17 Fluid, Electrolyte
- Page 546 and 547:
548 Chapter | 17 Fluid, Electrolyte
- Page 548 and 549:
550 Chapter | 17 Fluid, Electrolyte
- Page 551 and 552:
VIII. Clinicopathological Indicator
- Page 553 and 554:
References 555 plasma water, electr
- Page 555 and 556:
References 557 Krzywanek , H. ( 197
- Page 557 and 558:
References 559 Strombeck , D. R. (1
- Page 559 and 560:
562 Chapter | 18 Pituitary Function
- Page 561 and 562:
564 Chapter | 18 Pituitary Function
- Page 563 and 564:
566 Chapter | 18 Pituitary Function
- Page 565 and 566:
568 Chapter | 18 Pituitary Function
- Page 567 and 568:
570 Chapter | 18 Pituitary Function
- Page 569 and 570:
572 Chapter | 18 Pituitary Function
- Page 571 and 572:
574 Chapter | 18 Pituitary Function
- Page 573 and 574:
576 Chapter | 18 Pituitary Function
- Page 575 and 576:
578 Chapter | 18 Pituitary Function
- Page 577 and 578:
580 Chapter | 18 Pituitary Function
- Page 579 and 580:
582 Chapter | 18 Pituitary Function
- Page 581 and 582:
584 Chapter | 18 Pituitary Function
- Page 583 and 584:
586 Chapter | 18 Pituitary Function
- Page 585 and 586:
588 Chapter | 18 Pituitary Function
- Page 587 and 588:
590 Chapter | 18 Pituitary Function
- Page 589 and 590:
592 Chapter | 18 Pituitary Function
- Page 591 and 592:
594 Chapter | 18 Pituitary Function
- Page 593 and 594:
596 Chapter | 18 Pituitary Function
- Page 595 and 596:
598 Chapter | 18 Pituitary Function
- Page 597 and 598:
600 Chapter | 18 Pituitary Function
- Page 599 and 600:
602 Chapter | 18 Pituitary Function
- Page 601 and 602:
604 Chapter | 18 Pituitary Function
- Page 603 and 604:
606 Chapter | 19 Adrenocortical Fun
- Page 605 and 606:
608 Chapter | 19 Adrenocortical Fun
- Page 607 and 608:
610 Chapter | 19 Adrenocortical Fun
- Page 609 and 610:
612 Chapter | 19 Adrenocortical Fun
- Page 611 and 612:
614 Chapter | 19 Adrenocortical Fun
- Page 613 and 614:
616 Chapter | 19 Adrenocortical Fun
- Page 615 and 616:
618 Chapter | 19 Adrenocortical Fun
- Page 617 and 618:
620 Chapter | 19 Adrenocortical Fun
- Page 619 and 620:
622 Chapter | 19 Adrenocortical Fun
- Page 621 and 622:
624 Chapter | 20 Thyroid Function a
- Page 623 and 624:
626 Chapter | 20 Thyroid Function t
- Page 625 and 626:
628 Chapter | 20 Thyroid Function A
- Page 627 and 628:
630 Chapter | 20 Thyroid Function S
- Page 629 and 630:
632 Chapter | 20 Thyroid Function a
- Page 631 and 632:
634 Chapter | 20 Thyroid Function O
- Page 633 and 634:
636 Chapter | 21 Clinical Reproduct
- Page 635 and 636:
638 Chapter | 21 Clinical Reproduct
- Page 637 and 638:
640 Chapter | 21 Clinical Reproduct
- Page 639 and 640:
642 Chapter | 21 Clinical Reproduct
- Page 641 and 642:
644 Chapter | 21 Clinical Reproduct
- Page 643 and 644:
646 Chapter | 21 Clinical Reproduct
- Page 645 and 646:
648 Chapter | 21 Clinical Reproduct
- Page 647 and 648:
650 Chapter | 21 Clinical Reproduct
- Page 649 and 650:
652 Chapter | 21 Clinical Reproduct
- Page 651 and 652:
654 Chapter | 21 Clinical Reproduct
- Page 653 and 654:
656 Chapter | 21 Clinical Reproduct
- Page 655 and 656:
658 Chapter | 21 Clinical Reproduct
- Page 657 and 658:
660 Chapter | 21 Clinical Reproduct
- Page 659 and 660:
662 Chapter | 21 Clinical Reproduct
- Page 661 and 662:
664 Chapter | 22 Trace Minerals the
- Page 663 and 664:
666 Chapter | 22 Trace Minerals the
- Page 665 and 666:
668 Chapter | 22 Trace Minerals P i
- Page 667 and 668:
670 Chapter | 22 Trace Minerals be
- Page 669 and 670:
Copper Cuproreductase Cytochromes C
- Page 671 and 672:
674 Chapter | 22 Trace Minerals 2 .
- Page 673 and 674:
676 Chapter | 22 Trace Minerals Cor
- Page 675 and 676:
678 Chapter | 22 Trace Minerals inf
- Page 677 and 678:
680 Chapter | 22 Trace Minerals tis
- Page 679 and 680:
682 Chapter | 22 Trace Minerals VI
- Page 681 and 682:
684 Chapter | 22 Trace Minerals red
- Page 683 and 684:
686 Chapter | 22 Trace Minerals of
- Page 685 and 686:
688 Chapter | 22 Trace Minerals Per
- Page 687 and 688:
690 Chapter | 22 Trace Minerals In
- Page 689 and 690:
692 Chapter | 22 Trace Minerals Liu
- Page 691 and 692:
Chapter 23 Vitamins Robert B. Rucke
- Page 693 and 694:
III. Fat-Soluble Vitamins 697 TABLE
- Page 695 and 696:
III. Fat-Soluble Vitamins 699 Carot
- Page 697 and 698:
III. Fat-Soluble Vitamins 701 Major
- Page 699 and 700:
III. Fat-Soluble Vitamins 703 doses
- Page 701 and 702:
III. Fat-Soluble Vitamins 705 Diet
- Page 703 and 704:
III. Fat-Soluble Vitamins 707 conta
- Page 705 and 706:
III. Fat-Soluble Vitamins 709 immun
- Page 707 and 708:
IV. Water-Soluble Vitamins 711 are
- Page 709 and 710:
IV. Water-Soluble Vitamins 713 abil
- Page 711 and 712:
IV. Water-Soluble Vitamins 715 5’
- Page 713 and 714:
IV. Water-Soluble Vitamins 717 H 2
- Page 715 and 716:
IV. Water-Soluble Vitamins 719 Enzy
- Page 718 and 719:
722 Chapter | 23 Vitamins When biot
- Page 720 and 721:
724 Chapter | 23 Vitamins Cyanocoba
- Page 722 and 723:
726 Chapter | 23 Vitamins V . VITAM
- Page 724 and 725:
728 Chapter | 23 Vitamins nature, r
- Page 726 and 727:
730 Chapter | 23 Vitamins Stites ,
- Page 728 and 729:
732 Chapter | 24 Lysosomal Storage
- Page 730 and 731:
734 Chapter | 24 Lysosomal Storage
- Page 732 and 733:
736 Chapter | 24 Lysosomal Storage
- Page 734 and 735:
738 Chapter | 24 Lysosomal Storage
- Page 736 and 737:
740 Chapter | 24 Lysosomal Storage
- Page 738 and 739:
742 Chapter | 24 Lysosomal Storage
- Page 740 and 741:
744 Chapter | 24 Lysosomal Storage
- Page 742 and 743:
746 Chapter | 24 Lysosomal Storage
- Page 744 and 745:
748 Chapter | 24 Lysosomal Storage
- Page 746 and 747:
Chapter 25 Tumor Markers Michael D.
- Page 748 and 749:
II. Serum Tumor Markers 753 also be
- Page 750 and 751:
III. Flow Cytometry 755 cancer of t
- Page 752 and 753:
V. Immunohistochemistry/Immunocytoc
- Page 754 and 755:
V. Immunohistochemistry/Immunocytoc
- Page 756 and 757:
References 761 analysis will facili
- Page 758 and 759:
References 763 Fernandez , N. J. ,
- Page 760 and 761:
References 765 Meinecke , B. , and
- Page 762 and 763:
References 767 Walter , J. ( 2000 )
- Page 764 and 765:
770 Chapter | 26 Cerebrospinal Flui
- Page 766 and 767:
772 Chapter | 26 Cerebrospinal Flui
- Page 768 and 769:
774 Chapter | 26 Cerebrospinal Flui
- Page 770 and 771:
776 Chapter | 26 Cerebrospinal Flui
- Page 772 and 773:
778 Chapter | 26 Cerebrospinal Flui
- Page 774 and 775:
TABLE 26-7 Continued Constituent Ro
- Page 776 and 777:
782 Chapter | 26 Cerebrospinal Flui
- Page 778 and 779:
784 Chapter | 26 Cerebrospinal Flui
- Page 780 and 781:
786 Chapter | 26 Cerebrospinal Flui
- Page 782 and 783:
788 Chapter | 26 Cerebrospinal Flui
- Page 784 and 785:
790 Chapter | 26 Cerebrospinal Flui
- Page 786 and 787:
792 Chapter | 26 Cerebrospinal Flui
- Page 788 and 789:
794 Chapter | 26 Cerebrospinal Flui
- Page 790 and 791:
796 Chapter | 26 Cerebrospinal Flui
- Page 792 and 793:
798 Chapter | 26 Cerebrospinal Flui
- Page 794 and 795:
800 Chapter | 26 Cerebrospinal Flui
- Page 796 and 797:
802 Chapter | 26 Cerebrospinal Flui
- Page 798 and 799:
804 Chapter | 26 Cerebrospinal Flui
- Page 800 and 801:
806 Chapter | 26 Cerebrospinal Flui
- Page 802 and 803:
808 Chapter | 26 Cerebrospinal Flui
- Page 804 and 805:
810 Chapter | 26 Cerebrospinal Flui
- Page 806 and 807:
812 Chapter | 26 Cerebrospinal Flui
- Page 808 and 809:
814 Chapter | 26 Cerebrospinal Flui
- Page 810 and 811:
816 Chapter | 26 Cerebrospinal Flui
- Page 812 and 813:
818 Chapter | 26 Cerebrospinal Flui
- Page 814 and 815:
Chapter 27 Clinical Biochemistry in
- Page 816 and 817:
II. Hepatotoxicity 823 Therefore, A
- Page 818 and 819:
III. Nephrotoxicity 825 suggested a
- Page 820 and 821:
IV. Toxins Affecting Skeletal and C
- Page 822 and 823:
VII. Toxins Affecting Erythrocytes
- Page 824 and 825:
VIII. Toxins Affecting Hemoglobin a
- Page 826 and 827:
IX. Toxins Affecting the Nervous Sy
- Page 828 and 829:
References 835 Plants classified as
- Page 830 and 831:
References 837 Solaiman , S. G. , M
- Page 832 and 833:
840 Chapter | 28 Avian Clinical Bio
- Page 834 and 835:
842 Chapter | 28 Avian Clinical Bio
- Page 836 and 837:
844 Chapter | 28 Avian Clinical Bio
- Page 838 and 839:
846 Chapter | 28 Avian Clinical Bio
- Page 840 and 841:
848 Chapter | 28 Avian Clinical Bio
- Page 842 and 843:
850 Chapter | 28 Avian Clinical Bio
- Page 844 and 845:
Budgerigar ALAT (IU/g tissue) Budge
- Page 846 and 847:
854 Chapter | 28 Avian Clinical Bio
- Page 848 and 849:
856 Chapter | 28 Avian Clinical Bio
- Page 850 and 851:
858 Chapter | 28 Avian Clinical Bio
- Page 852 and 853:
860 Chapter | 28 Avian Clinical Bio
- Page 854 and 855:
862 Chapter | 28 Avian Clinical Bio
- Page 856 and 857:
864 Chapter | 28 Avian Clinical Bio
- Page 858 and 859:
866 Chapter | 28 Avian Clinical Bio
- Page 860 and 861:
868 Chapter | 28 Avian Clinical Bio
- Page 862 and 863:
870 Chapter | 28 Avian Clinical Bio
- Page 864 and 865:
872 Chapter | 28 Avian Clinical Bio
- Page 866 and 867:
874 Appendix | I SI Units TABLE E S
- Page 868 and 869:
Appendix II Conversion Factors of S
- Page 870 and 871:
Appendix IV Stability of Serum Enzy
- Page 872 and 873:
Appendix VI Nomogram for Computing
- Page 874 and 875:
t0100 Appendix VIII Blood Analyte R
- Page 876 and 877:
884 Appendix | VIII Blood Analyte R
- Page 878 and 879:
886 Appendix | VIII Blood Analyte R
- Page 880 and 881:
888 Appendix | VIII Blood Analyte R
- Page 882 and 883:
890 Appendix | IX Blood Analyte Ref
- Page 884 and 885:
892 Appendix | IX Blood Analyte Ref
- Page 886 and 887:
894 Appendix | IX Blood Analyte Ref
- Page 888 and 889:
Appendix X Blood Analyte Reference
- Page 890 and 891:
Appendix XI Blood Analyte Reference
- Page 892 and 893:
Appendix XII Urine Analyte Referenc
- Page 894 and 895:
902 Appendix | XIII Cerebrospinal F
- Page 896:
904 Appendix | XIV Cerebrospinal Fl