Inzien en bewijzen - CWI

24 HOOFDSTUK 2. (IN)ZIEN EN BEWIJZEN
Als je de andere bewijzen met elkaar vergelijkt, dan zie je dat ze steeds andere verbanden
leggen. Een nieuw bewijs van iets wat je al hebt ingezien kan dus toch voor nieuw inzicht zorgen,
doordat het nieuwe verbanden legt tussen dingen die je al weet.
2.5 Meer bewijzen, meer inzicht
b
C
F G
E
e
d
D
A B
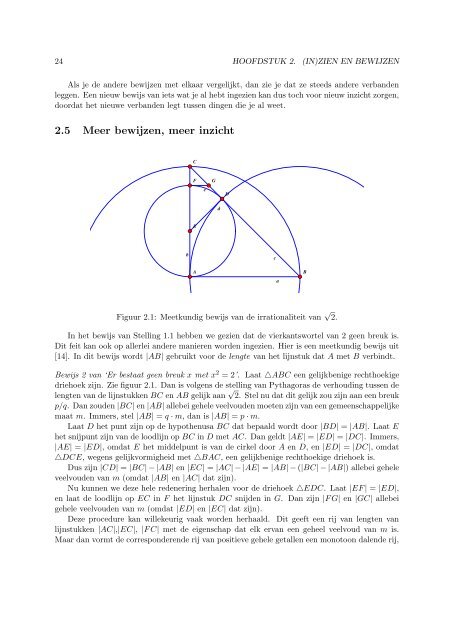
Figuur 2.1: Meetkundig bewijs van de irrationaliteit van √ 2.
In het bewijs van Stelling 1.1 hebben we gezien dat de vierkantswortel van 2 geen breuk is.
Dit feit kan ook op allerlei andere manieren worden ingezien. Hier is een meetkundig bewijs uit
[14]. In dit bewijs wordt |AB| gebruikt voor de lengte van het lijnstuk dat A met B verbindt.
Bewijs 2 van ‘Er bestaat geen breuk x met x 2 = 2’. Laat △ABC een gelijkbenige rechthoekige
driehoek zijn. Zie figuur 2.1. Dan is volgens de stelling van Pythagoras de verhouding tussen de
lengten van de lijnstukken BC en AB gelijk aan √ 2. Stel nu dat dit gelijk zou zijn aan een breuk
p/q. Dan zouden |BC| en |AB| allebei gehele veelvouden moeten zijn van een gemeenschappelijke
maat m. Immers, stel |AB| = q · m, dan is |AB| = p · m.
Laat D het punt zijn op de hypothenusa BC dat bepaald wordt door |BD| = |AB|. Laat E
het snijpunt zijn van de loodlijn op BC in D met AC. Dan geldt |AE| = |ED| = |DC|. Immers,
|AE| = |ED|, omdat E het middelpunt is van de cirkel door A en D, en |ED| = |DC|, omdat
△DCE, wegens gelijkvormigheid met △BAC, een gelijkbenige rechthoekige driehoek is.
Dus zijn |CD| = |BC| − |AB| en |EC| = |AC| − |AE| = |AB| − (|BC| − |AB|) allebei gehele
veelvouden van m (omdat |AB| en |AC| dat zijn).
Nu kunnen we deze hele redenering herhalen voor de driehoek △EDC. Laat |EF | = |ED|,
en laat de loodlijn op EC in F het lijnstuk DC snijden in G. Dan zijn |F G| en |GC| allebei
gehele veelvouden van m (omdat |ED| en |EC| dat zijn).
Deze procedure kan willekeurig vaak worden herhaald. Dit geeft een rij van lengten van
lijnstukken |AC|,|EC|, |F C| met de eigenschap dat elk ervan een geheel veelvoud van m is.
Maar dan vormt de corresponderende rij van positieve gehele getallen een monotoon dalende rij,
c
a