Diplomarbeit von Michael Schindler

0
(a)
1.1 Dichteschätzung mit einer Mischung multivariater Normalverteilungen 25
t = 0
0.4
50 T 80 T 100 T
2
0
max
C
σ(t)
l(C, σ�X)
−2
−4
(b)
t = 0 50 T 80 T 100 T
1
0
1
(c1)
[cr]1(t)
[cr]2(t)
0
(c2)
0 t=50 T 80 T 100 T
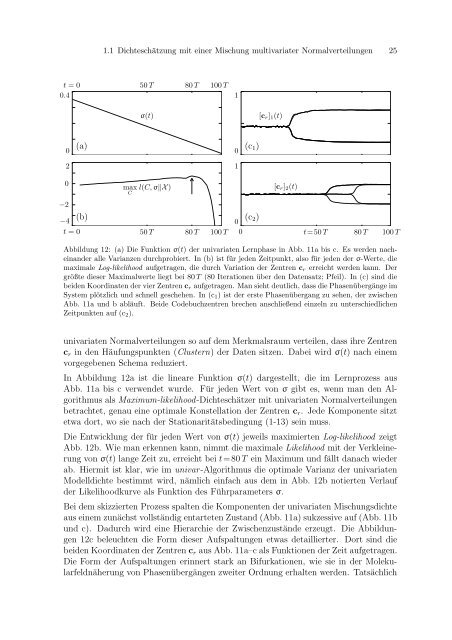
Abbildung 12: (a) Die Funktion σ(t) der univariaten Lernphase in Abb. 11a bis c. Es werden nacheinander
alle Varianzen durchprobiert. In (b) ist für jeden Zeitpunkt, also für jeden der σ-Werte, die
maximale Log-likelihood aufgetragen, die durch Variation der Zentren cr erreicht werden kann. Der
größte dieser Maximalwerte liegt bei 80 T (80 Iterationen über den Datensatz; Pfeil). In (c) sind die
beiden Koordinaten der vier Zentren cr aufgetragen. Man sieht deutlich, dass die Phasenübergänge im
System plötzlich und schnell geschehen. In (c1) ist der erste Phasenübergang zu sehen, der zwischen
Abb. 11a und b abläuft. Beide Codebuchzentren brechen anschließend einzeln zu unterschiedlichen
Zeitpunkten auf (c2).
univariaten Normalverteilungen so auf dem Merkmalsraum verteilen, dass ihre Zentren
cr in den Häufungspunkten (Clustern) der Daten sitzen. Dabei wird σ(t) nach einem
vorgegebenen Schema reduziert.
In Abbildung 12a ist die lineare Funktion σ(t) dargestellt, die im Lernprozess aus
Abb. 11a bis c verwendet wurde. Für jeden Wert von σ gibt es, wenn man den Algorithmus
als Maximum-likelihood-Dichteschätzer mit univariaten Normalverteilungen
betrachtet, genau eine optimale Konstellation der Zentren cr. Jede Komponente sitzt
etwa dort, wo sie nach der Stationaritätsbedingung (1-13) sein muss.
Die Entwicklung der für jeden Wert von σ(t) jeweils maximierten Log-likelihood zeigt
Abb. 12b. Wie man erkennen kann, nimmt die maximale Likelihood mit der Verkleinerung
von σ(t) lange Zeit zu, erreicht bei t=80 T ein Maximum und fällt danach wieder
ab. Hiermit ist klar, wie im univar-Algorithmus die optimale Varianz der univariaten
Modelldichte bestimmt wird, nämlich einfach aus dem in Abb. 12b notierten Verlauf
der Likelihoodkurve als Funktion des Führparameters σ.
Bei dem skizzierten Prozess spalten die Komponenten der univariaten Mischungsdichte
aus einem zunächst vollständig entarteten Zustand (Abb. 11a) sukzessive auf (Abb. 11b
und c). Dadurch wird eine Hierarchie der Zwischenzustände erzeugt. Die Abbildungen
12c beleuchten die Form dieser Aufspaltungen etwas detaillierter. Dort sind die
beiden Koordinaten der Zentren cr aus Abb. 11a–c als Funktionen der Zeit aufgetragen.
Die Form der Aufspaltungen erinnert stark an Bifurkationen, wie sie in der Molekularfeldnäherung
von Phasenübergängen zweiter Ordnung erhalten werden. Tatsächlich