Diplomarbeit von Michael Schindler

64 2. On-line Lernen mit univar
immer möglich, während es in den anderen Fällen zu Diskretisierungseffekten kommen
kann.
Bei großen τS ≫ 1 wird die grobskalige Definition (Typ II) des Phasenübergangs verwendet,
die von dem Minimalabstand s˜σ aus (2-29) abhängt (vgl. wieder Abb. 26c1).
Durch die Diskretisierung werden lediglich kleine Fluktuationen auf diesen Abstand
übertragen. Dabei wird die Phasenübergangskurve jedoch nicht verändert, denn bei
τS ≫1 wird der genaue Wert des Codebuchabstandes am Umkehrpunkt unwichtig, wie
wir an Abb. 31 sehen konnten.
Es bleibt also nur der Bereich mittlerer Zeiten τS ≈ 1, wo die infinitesimale Definition
(Typ I) des Phasenübergangs verwendet wird, in dem Diskretisierungseffekte eine
Rolle spielen können. Dort kann es vorkommen, dass große Werte von ε auf kurze
Lebensdauern TS treffen (etwa TS = 5 und ε = 1/5). In solchen Fällen ist die Annahme
(2-22) nicht mehr gültig, und man muss Gleichung (2-27), welche die Abhängigkeit
der kritischen Parameter voneinander beschreibt, durch ihre diskrete Version ersetzen,
σkrit(TS, ε)
σS
=
�
1 +
1 − (1−ε/2)TS
1 + (1−ε/2) TS
� �
1
TS
1 − (1−ε/2) 2TS
1 − (1−ε/2) 2
. (2-30)
Diese Gleichung wird in Appendix B.2 durch Übertragung der Überlegungen zu dem
kontinuierlichen auf den diskreten Fall gefunden.
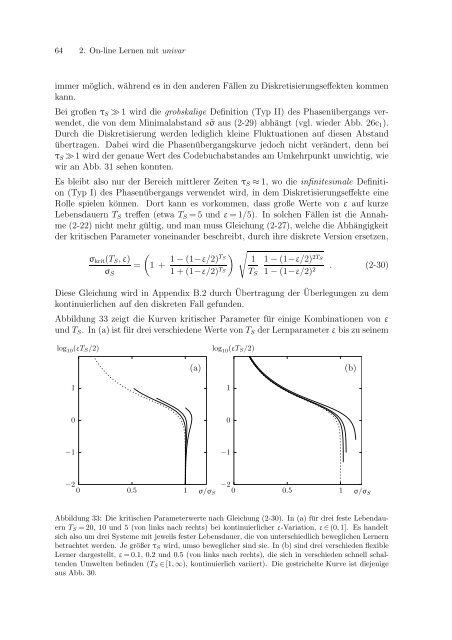
Abbildung 33 zeigt die Kurven kritischer Parameter für einige Kombinationen von ε
und TS. In (a) ist für drei verschiedene Werte von TS der Lernparameter ε bis zu seinem
log 10(εTS/2)
1
0
−1
(a)
−2
0 0.5 1 σ/σS
log 10(εTS/2)
1
0
−1
(b)
−2
0 0.5 1 σ/σS
Abbildung 33: Die kritischen Parameterwerte nach Gleichung (2-30). In (a) für drei feste Lebendauern
TS = 20, 10 und 5 (von links nach rechts) bei kontinuierlicher ε-Variation, ε ∈(0, 1]. Es handelt
sich also um drei Systeme mit jeweils fester Lebensdauer, die von unterschiedlich beweglichen Lernern
betrachtet werden. Je größer τS wird, umso beweglicher sind sie. In (b) sind drei verschieden flexible
Lerner dargestellt, ε = 0.1, 0.2 und 0.5 (von links nach rechts), die sich in verschieden schnell schaltenden
Umwelten befinden (TS ∈[1, ∞), kontinuierlich variiert). Die gestrichelte Kurve ist diejenige
aus Abb. 30.