Thermodynamique (2004-2010). - Université de Genève

où δv et δx sont respectivement les incertitudes sur la vitesse et de la position, m est la
masse de la particule, et = 1.05457266·10 −34 (Js) est la constante de Planck. Imaginons
qu’à un certain moment nous posons notre particule à un certain endroit bien défini.
Appelons ce temps t = 0, et la position x = 0. A ce moment, l’incertitude dans la position
de notre particule est nulle. La particule se trouve dans une distribution de probabilité
P (x, t = 0) qui correspond à une fonction δ(x) qui est infiniment étroite, et dont l’aire est
1. Suivant le principe d’incertitude, la vitesse peut prendre n’importe quelle valeur, donc
avec le temps P (x, t) va rapidement élargir. Pour simplifier la notation nous indiquerons
désormais la largeur spatiale u = δx. La largeur de la vitesse δv n’est rien d’autre que la
dérivée par rapport au temps de la largeur spatiale, donc δv = du/dt. Conséquemment la
relation d’incertitude s’écrit
udu/dt ≥ /m
La règle de la chaine nous indique que du 2 /dt = 2udu/dt, ce qui permet de résoudre la
relation d’incertitude par intégration
u ≥
2
m
· t (9.2)
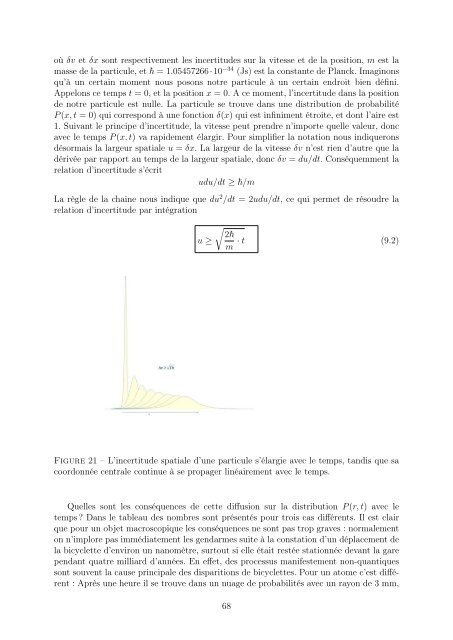
Figure 21 – L’incertitude spatiale d’une particule s’élargie avec le temps, tandis que sa
coordonnée centrale continue à se propager linéairement avec le temps.
Quelles sont les conséquences de cette diffusion sur la distribution P (r, t) avec le
temps ? Dans le tableau des nombres sont présentés pour trois cas différents. Il est clair
que pour un objet macroscopique les conséquences ne sont pas trop graves : normalement
on n’implore pas immédiatement les gendarmes suite à la constation d’un déplacement de
la bicyclette d’environ un nanomètre, surtout si elle était restée stationnée devant la gare
pendant quatre milliard d’années. En effet, des processus manifestement non-quantiques
sont souvent la cause principale des disparitions de bicyclettes. Pour un atome c’est différent
: Après une heure il se trouve dans un nuage de probabilités avec un rayon de 3 mm,
68