Beugung und Interferenz - Walther Meißner Institut

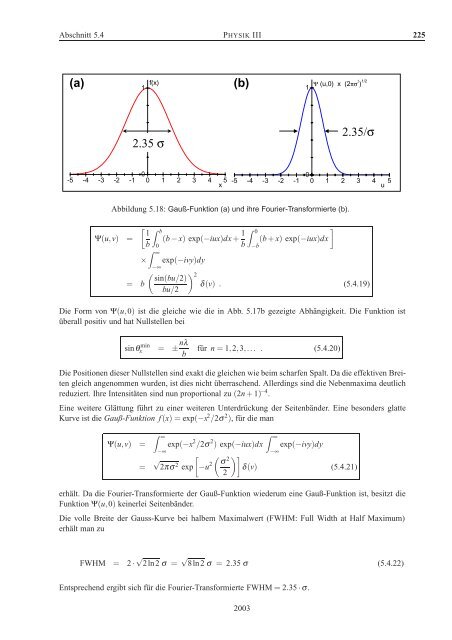
Abschnitt 5.4 PHYSIK III 225(a)1f(x)(b)1Ψ (u,0) x (2πσ 2 ) 1/22.35 σ2.35/σ0-5 -4 -3 -2 -1 0 1 2 3 4 5x0-5 -4 -3 -2 -1 0 1 2 3 4 5uAbbildung 5.18: Gauß-Funktion (a) und ihre Fourier-Transformierte (b).[ ∫ 1 bΨ(u,v) = (b − x) exp(−iux)dx+ 1 ∫ 0](b + x) exp(−iux)dxb 0b −b∫ ∞× exp(−ivy)dy−∞( ) sin(bu/2) 2= bδ(v) . (5.4.19)bu/2Die Form von Ψ(u,0) ist die gleiche wie die in Abb. 5.17b gezeigte Abhängigkeit. Die Funktion istüberall positiv und hat Nullstellen beisin θ minx = ± nλ bfür n = 1,2,3,... . (5.4.20)Die Positionen dieser Nullstellen sind exakt die gleichen wie beim scharfen Spalt. Da die effektiven Breitengleich angenommen wurden, ist dies nicht überraschend. Allerdings sind die Nebenmaxima deutlichreduziert. Ihre Intensitäten sind nun proportional zu (2n + 1) −4 .Eine weitere Glättung führt zu einer weiteren Unterdrückung der Seitenbänder. Eine besonders glatteKurve ist die Gauß-Funktion f (x)=exp(−x 2 /2σ 2 ),für die man∫ ∞Ψ(u,v) = exp(−x 2 /2σ 2 ) exp(−iux)dx exp(−ivy)dy−∞−∞= √ ( )] σ2πσ 2 exp[−u 2 2δ(v) (5.4.21)2erhält. Da die Fourier-Transformierte der Gauß-Funktion wiederum eine Gauß-Funktion ist, besitzt dieFunktion Ψ(u,0) keinerlei Seitenbänder.Die volle Breite der Gauss-Kurve bei halbem Maximalwert (FWHM: Full Width at Half Maximum)erhält man zu∫ ∞FWHM = 2 · √2ln2σ= √ 8ln2σ = 2.35 σ (5.4.22)Entsprechend ergibt sich für die Fourier-Transformierte FWHM = 2.35 · σ.2003