Beugung und Interferenz - Walther Meißner Institut

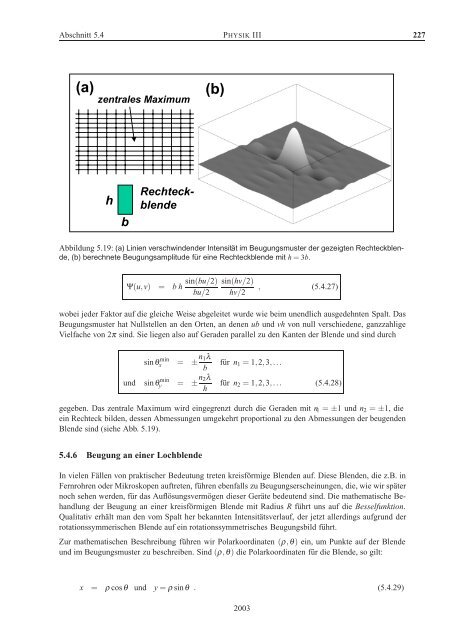
Abschnitt 5.4 PHYSIK III 227(a)zentrales Maximum(b)hbRechteckblendeAbbildung 5.19: (a) Linien verschwindender Intensität im Beugungsmuster der gezeigten Rechteckblende,(b) berechnete Beugungsamplitude für eine Rechteckblende mit h = 3b.Ψ(u,v) = bh sin(bu/2)bu/2sin(hv/2)hv/2, (5.4.27)wobei jeder Faktor auf die gleiche Weise abgeleitet wurde wie beim unendlich ausgedehnten Spalt. DasBeugungsmuster hat Nullstellen an den Orten, an denen ub und vh von null verschiedene, ganzzahligeVielfache von 2π sind. Sie liegen also auf Geraden parallel zu den Kanten der Blende und sind durchundsinθx min = ± n 1λbsinθy min = ± n 2λhfür n 1 = 1,2,3,...für n 2 = 1,2,3,... (5.4.28)gegeben. Das zentrale Maximum wird eingegrenzt durch die Geraden mit n 1 = ±1 und n 2 = ±1, dieein Rechteck bilden, dessen Abmessungen umgekehrt proportional zu den Abmessungen der beugendenBlende sind (siehe Abb. 5.19).5.4.6 Beugung an einer LochblendeIn vielen Fällen von praktischer Bedeutung treten kreisförmige Blenden auf. Diese Blenden, die z.B. inFernrohren oder Mikroskopen auftreten, führen ebenfalls zu Beugungserscheinungen, die, wie wir späternoch sehen werden, für das Auflösungsvermögen dieser Geräte bedeutend sind. Die mathematische Behandlungder Beugung an einer kreisförmigen Blende mit Radius R führt uns auf die Besselfunktion.Qualitativ erhält man den vom Spalt her bekannten Intensitätsverlauf, der jetzt allerdings aufgrund derrotationssymmerischen Blende auf ein rotationssymmetrisches Beugungsbild führt.Zur mathematischen Beschreibung führen wir Polarkoordinaten (ρ,θ) ein, um Punkte auf der Blendeund im Beugungsmuster zu beschreiben. Sind (ρ,θ) die Polarkoordinaten für die Blende, so gilt:x = ρ cos θ und y = ρ sinθ . (5.4.29)2003