Beugung und Interferenz - Walther Meißner Institut

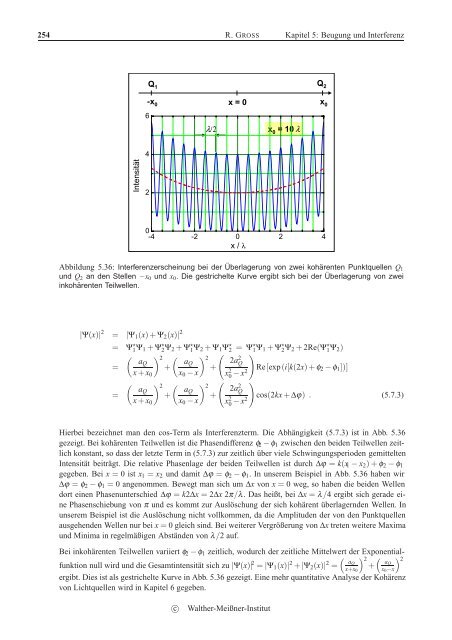
254 R. GROSS Kapitel 5: Beugung und InterferenzQ 1Q 2-x 0 x = 0x 06λ/2 x 0 = 10 λ4Intensität20-4 -2 0 2 4x / λAbbildung 5.36: Interferenzerscheinung bei der Überlagerung von zwei kohärenten Punktquellen Q 1und Q 2 an den Stellen −x 0 und x 0 . Die gestrichelte Kurve ergibt sich bei der Überlagerung von zweiinkohärenten Teilwellen.|Ψ(x)| 2 = |Ψ 1 (x)+Ψ 2 (x)| 2= Ψ ⋆ 1Ψ 1 + Ψ ⋆ 2Ψ 2 + Ψ ⋆ 1Ψ 2 + Ψ 1 Ψ ⋆ 2 = Ψ ⋆ 1Ψ 1 + Ψ ⋆ 2Ψ 2 + 2Re(Ψ ⋆ 1Ψ 2 )( ) 2 ( ) ( )2 aQ aQ 2a2Q=+ +x + x 0 x 0 − x x 2 0 − Re[exp (i[k(2x)+φ 2 − φ 1 ])]x2( ) 2 ( ) ( )2 aQ aQ 2a2Q=+ +x + x 0 x 0 − x x 2 0 − cos(2kx+ ∆ϕ) . (5.7.3)x2Hierbei bezeichnet man den cos-Term als Interferenzterm. Die Abhängigkeit (5.7.3) ist in Abb. 5.36gezeigt. Bei kohärenten Teilwellen ist die Phasendifferenz φ 2 − φ 1 zwischen den beiden Teilwellen zeitlichkonstant, so dass der letzte Term in (5.7.3) zur zeitlich über viele Schwingungsperioden gemitteltenIntensität beiträgt. Die relative Phasenlage der beiden Teilwellen ist durch ∆ϕ = k(x 1 − x 2 )+φ 2 − φ 1gegeben. Bei x = 0 ist x 1 = x 2 und damit ∆ϕ = φ 2 − φ 1 . In unserem Beispiel in Abb. 5.36 haben wir∆ϕ = φ 2 − φ 1 = 0 angenommen. Bewegt man sich um ∆x von x = 0 weg, so haben die beiden Wellendort einen Phasenunterschied ∆ϕ = k2∆x = 2∆x 2π/λ. Das heißt, bei ∆x = λ/4 ergibt sich gerade einePhasenschiebung von π und es kommt zur Auslöschung der sich kohärent überlagernden Wellen. Inunserem Beispiel ist die Auslöschung nicht vollkommen, da die Amplituden der von den Punktquellenausgehenden Wellen nur bei x = 0 gleich sind. Bei weiterer Vergrößerung von ∆x treten weitere Maximaund Minima in regelmäßigen Abständen von λ/2 auf.Bei inkohärenten Teilwellen variiert φ 2 − φ 1 zeitlich, wodurch der zeitliche Mittelwert der Exponentialfunktionnull wird und die Gesamtintensität sich zu |Ψ(x)| 2 = |Ψ 1 (x)| 2 +|Ψ 2 (x)| 2 aQ 2 ( )( )aQ2=x+x 0+x 0 −xergibt. Dies ist als gestrichelte Kurve in Abb. 5.36 gezeigt. Eine mehr quantitative Analyse der Kohärenzvon Lichtquellen wird in Kapitel 6 gegeben.c○Walther-Meißner-Institut