Appunti per il corso: Fisica del plasma di quark e gluoni (A.A. ... - Infn
Appunti per il corso: Fisica del plasma di quark e gluoni (A.A. ... - Infn
Appunti per il corso: Fisica del plasma di quark e gluoni (A.A. ... - Infn
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
cosi come<br />
p (5) = (E, 0, π/a, pz), p (6) = (E, 0, π, π/a − pz), p (7) = (E, π/a, π/a, pz),<br />
p (8) = (E, π/a, π/a, π/a − pz) (9.40)<br />
sod<strong>di</strong>sfano la regola <strong>di</strong> <strong>di</strong>s<strong>per</strong>sione. Quin<strong>di</strong> ogni fermione <strong>di</strong> energia assegnata E risulta 8 volte degenere. Ci sono<br />
varie soluzioni a questo problema, ma nessuna particolarmente sod<strong>di</strong>sfacente. Il problema ha a che fare con <strong>il</strong> fatto<br />
che è in pratica impossib<strong>il</strong>e evitare <strong>il</strong> problema <strong>di</strong> queste soluzioni spurie (problema <strong>del</strong> doubling) senza rom<strong>per</strong>e<br />
esplicitamente la simmetria chirale. Considereremo qui la soluzione <strong>di</strong> W<strong>il</strong>son. Questa consiste nell’introdurre un<br />
termine che è un termine <strong>di</strong> massa sul reticolo, ma che si <strong>di</strong>saccoppia nel limite <strong>del</strong> continuo. Il termine è<br />
Nello spazio degli impulsi l’o<strong>per</strong>atore <strong>di</strong> Dirac <strong>di</strong>venta<br />
1 <br />
¯ψnψn+ˆµ +<br />
2a<br />
¯ ψn+ˆµψn − 2 ¯ <br />
ψnψn<br />
i <br />
µ<br />
µ sin akµ<br />
γ +<br />
a<br />
cos akµ − 1<br />
a<br />
µ<br />
Notiamo che mentre <strong>il</strong> primo termine tende all’o<strong>per</strong>atore <strong>di</strong> Dirac <strong>per</strong> a → 0 <strong>il</strong> secondo termine va a zero come a.<br />
Il termine <strong>di</strong> W<strong>il</strong>son mo<strong>di</strong>fica l’andamento <strong>del</strong> propagatore agli estremi <strong>del</strong>la zona <strong>di</strong> Br<strong>il</strong>louin eliminando lo zero .<br />
Infatti <strong>il</strong> propagatore è essenzialmente l’inverso <strong>di</strong> (considerando una sola <strong>di</strong>mensione)<br />
sin 2 akµ<br />
a 2<br />
+ (cos akµ − 1) 2<br />
a 2<br />
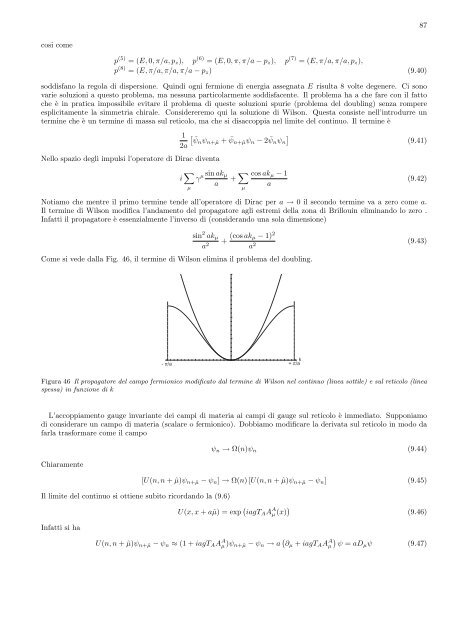
Come si vede dalla Fig. 46, <strong>il</strong> termine <strong>di</strong> W<strong>il</strong>son elimina <strong>il</strong> problema <strong>del</strong> doubling.<br />
- π/a<br />
Figura 46 Il propagatore <strong>del</strong> campo fermionico mo<strong>di</strong>ficato dal termine <strong>di</strong> W<strong>il</strong>son nel continuo (linea sott<strong>il</strong>e) e sul reticolo (linea<br />
spessa) in funzione <strong>di</strong> k<br />
L’accoppiamento gauge invariante dei campi <strong>di</strong> materia ai campi <strong>di</strong> gauge sul reticolo è imme<strong>di</strong>ato. Supponiamo<br />
<strong>di</strong> considerare un campo <strong>di</strong> materia (scalare o fermionico). Dobbiamo mo<strong>di</strong>ficare la derivata sul reticolo in modo da<br />
farla trasformare come <strong>il</strong> campo<br />
Chiaramente<br />
Il limite <strong>del</strong> continuo si ottiene subito ricordando la (9.6)<br />
Infatti si ha<br />
ψn → Ω(n)ψn<br />
+ π/a k<br />
87<br />
(9.41)<br />
(9.42)<br />
(9.43)<br />
(9.44)<br />
[U(n, n + ˆµ)ψn+ˆµ − ψn] → Ω(n) [U(n, n + ˆµ)ψn+ˆµ − ψn] (9.45)<br />
U(x, x + aˆµ) = exp iagTAA A µ (x) <br />
(9.46)<br />
U(n, n + ˆµ)ψn+ˆµ − ψn ≈ (1 + iagTAA A µ )ψn+ˆµ − ψn → a ∂µ + iagTAA A <br />
µ ψ = aDµψ (9.47)