PE EIE[R-Rg RESEARCH ON - HJ Andrews Experimental Forest

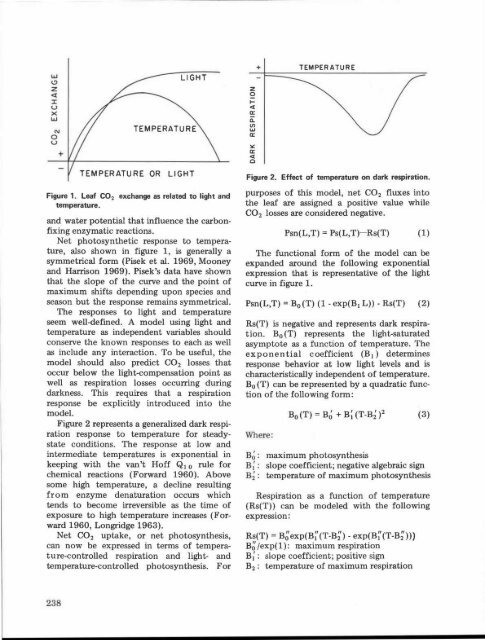
Figure 2. Effect of temperature on dark respiration .
Figure 1 . Leaf CO2 exchange as related to light an d
temperature .
and water potential that influence the carbon -
fixing enzymatic reactions .
Net photosynthetic response to temperature,
also shown in figure 1, is generally a
symmetrical form (Pisek et al . 1969, Moone y
and Harrison 1969). Pisek's data have show n
that the slope of the curve and the point of
maximum shifts depending upon species an d
season but the response remains symmetrical .
The responses to light and temperatur e
seem well-defined. A model using light an d
temperature as independent variables shoul d
conserve the known responses to each as wel l
as include any interaction . To be useful, th e
model should also predict CO 2 losses that
occur below the light-compensation point a s
well as respiration losses occurring durin g
darkness . This requires that a respiratio n
response be explicitly introduced into th e
model.
Figure 2 represents a generalized dark respiration
response to temperature for steady -
state conditions. The response at low an d
intermediate temperatures is exponential i n
keeping with the van 't Hoff Q 1 o rule for
chemical reactions (Forward 1960). Abov e
some high temperature, a decline resultin g
from enzyme denaturation occurs which
tends to become irreversible as the time o f
exposure to high temperature increases (For -
ward 1960, Longridge 1963) .
Net CO 2 uptake, or net photosynthesis ,
can now be expressed in terms of temperature-controlled
respiration and light- an d
temperature-controlled photosynthesis . For
purposes of this model, net CO 2 fluxes int o
the leaf are assigned a positive value whil e
CO 2 losses are considered negative .
Psn(L,T) = Ps(L,T)-Rs(T) (1)
The functional form of the model can b e
expanded around the following exponential
expression that is representative of the ligh t
curve in figure 1 .
Psn(L,T) = Bo(T) (1 - exp(B 1 L)) - Rs(T) (2 )
Rs(T) is negative and represents dark respiration
. Bo(T) represents the light-saturate d
asymptote as a function of temperature . Th e
exponential coefficient (B 1 ) determine s
response behavior at low light levels and is
characteristically independent of temperature .
Bo (T) can be represented by a quadratic function
of the following form :
Where :
B o (T) = Bo + B i (T-B ) 2 (3 )
Bo : maximum photosynthesi s
B ; : slope coefficient ; negative algebraic sign
B2 : temperature of maximum photosynthesi s
Respiration as a function of temperature
(Rs(T)) can be modeled with the followin g
expression :
Rs(T) = Boexp(BI (T-B.) - exp(BI (T-B . )) )
Bo /exp(1) : maximum respiratio n
B1 : slope coefficient ; positive sign
B 2 : temperature of maximum respiratio n
238