Application and Optimisation of the Spatial Phase Shifting ...

More documents

Recommendations

Info

114 Comparison of noise in phase maps from TPS and SPS within 5% when this technique was used. The subtraction method is known as „dark frame“ calibration method [Che85]. Note here that both SPS and TPS are implemented as integrating-bucket versions. 5.2 Preliminary investigations To obtain the best performance for both of the methods, some experimental parameters have to be fixed. These are the phase shift to work with and the optimal reference-to-object intensity ratio. The latter will be treated in Chapter 6.1.1 in a wider context; for now, let us retain that the standard beam ratio B=R /O is 10:1 in this chapter. Also, it is important to get to know the test object and to assess the reliability of the results. The preliminary steps are briefly described below. 5.2.1 Choice of phase shift Since it is essential for light efficiency to keep the speckles as small as possible, the number of phase sampling points for SPS is restricted to the minimum, which is three (see Chapter 3.2). Therefore, we use a three-phase formula also in TPS. For this number of samples, the two common values for the phase shift to choose from are α=90° or α=120°. Theoretical results [Cre88, Sur97a] suggest that for TPS, 120° should be the better choice. For SPS however, the findings of Chapter 3.2.2 indicate an advantage for α=90°. 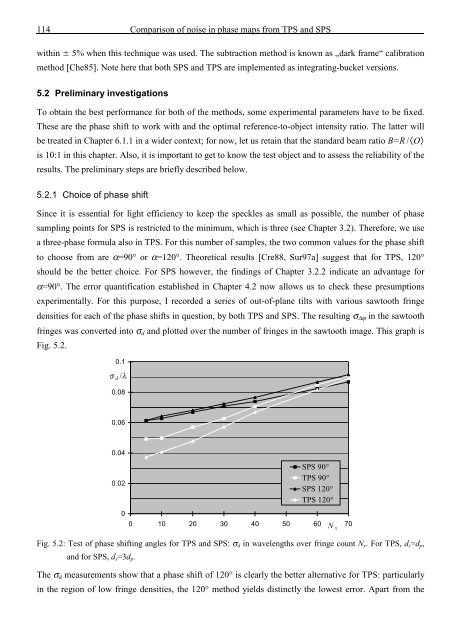The error quantification established in Chapter 4.2 now allows us to check these presumptions experimentally. For this purpose, I recorded a series of out-of-plane tilts with various sawtooth fringe densities for each of the phase shifts in question, by both TPS and SPS. The resulting σ ∆ϕ in the sawtooth fringes was converted into σ d and plotted over the number of fringes in the sawtooth image. This graph is Fig. 5.2. 0.1 σ d /λ 0.08 0.06 0.04 0.02 0 SPS 90° TPS 90° SPS 120° TPS 120° 0 10 20 30 40 50 60 70 N x Fig. 5.2: Test of phase shifting angles for TPS and SPS: σ d in wavelengths over fringe count N x . For TPS, d s =d p , and for SPS, d s =3d p . The σ d measurements show that a phase shift of 120° is clearly the better alternative for TPS: particularly in the region of low fringe densities, the 120° method yields distinctly the lowest error. Apart from the
5.2 Preliminary investigations 115 generally higher noise level, the accuracy of the SPS measurements shows a less pronounced dependence on the phase shift. Moreover, the 90° formula performs slightly better, in contrast to the theoretical findings in [Bot97], but in agreement with the more speckle-specific investigations in Chapter 3.2.2. The slight difference in performance does however not appear to discourage using 120° also for SPS in this study, and we will do so to maintain comparability, but will come back to α=90° in SPS in Chapter 6.1.2. For higher fringe densities, TPS and SPS deliver similar performance; this is partly due to the aforementioned fact that significant speckle displacement occurs for larger tilts, which contributes the larger part to speckle decorrelation when the speckles are small. 5.2.2 Reproducibility of the σ d values While the fitting algorithm described in Chapter 4.2 yields a very reliable average of phase errors in one sawtooth image, this tells us nothing about whether we will get the same error in a second experiment. This deserves particular attention because the test object had not been specially made: it was a large mirror mount onto which a rotation stage was fitted with the aluminium plate on it. The out-of-plane tilts were generated by manual setting via the fine-thread screws of the mirror mount, and the in-plane rotations by manual setting of the rotation stage via a reduction gear. While the latter yielded excellent reproducibility of the measured displacement errors, the former showed some fluctuations, which had to be investigated in more detail to learn how reliable the σ d measurements are. Fig. 5.3 shows the results for a set of SPS experiments. For each of the speckle sizes 1.5, 3, and 6 d p , the tilt sequence was repeated 10 times; the averages σ d with their respective standard deviations σσ d are given in the figure. This was done for both vertical and horizontal sawtooth fringes. 0.12 σ d ¡ /λ Tilt about y axis 12 Tilt about x axis 0.1 1 0.08 08 0.06 0.04 d s =1.5 d p d s =3 d p 04 0 20 40 60 80 N x 100 06 d s =1.5 d p d s =3 d p d s =6 d p 0 20 40 60 80 N y 100 Fig. 5.3: Reproducibility of measurements of σ d vs. N x and N y for out-of-plane tilts. Left: tilt about y-axis, vertical fringes; right: tilt about x-axis, horizontal fringes. Note that the ordinates begin at σ d = 0.04 λ to expand the error bars. For a speckle size of 6 d p , the reproducibility is excellent. At low fringe densities, the spatial phase measurement works well because of the low intensity and phase gradients in the speckles; but as the tilt increases, aperture-plane decorrelation impairs the accuracy. For d s =6 d p , the σ d curves are very similar
Page 1 and 2:
Application and Optimisation of the
Page 3 and 4:
Table of Contents 1 1 INTRODUCTION
Page 5 and 6:
3 1 Introduction The present era of
Page 7 and 8:
Introduction 5 retrieval can help t
Page 9 and 10:
7 2 Statistical Properties of Speck
Page 11 and 12:
2.1 Experimental set-up 9 Gaussian
Page 13 and 14:
2.2 First-order speckle statistics
Page 15 and 16:
Page 17 and 18:
Page 19 and 20:
Page 21 and 22:
Page 23 and 24:
Page 25 and 26:
Page 27 and 28:
Page 29 and 30:
Page 31 and 32:
Page 33 and 34:
Page 35 and 36:
2.3 Second-order speckle statistics
Page 37 and 38:
Page 39 and 40:
Page 41 and 42:
Page 43 and 44:
Page 45 and 46:
Page 47 and 48:
Page 49 and 50:
47 3 Electronic or Digital Speckle
Page 51 and 52:
3.1 Subtraction-mode ESPI 49 some 4
Page 53 and 54:
3.2 Phase-shifting ESPI 51 filled u
Page 55 and 56:
3.2 Phase-shifting ESPI 53 known si
Page 57 and 58:
3.2 Phase-shifting ESPI 55 α n =α
Page 59 and 60:
3.2 Phase-shifting ESPI 57 But reme
Page 61 and 62:
3.2 Phase-shifting ESPI 59 ϕ ϕ O,
Page 63 and 64:
3.2 Phase-shifting ESPI 61 These fo
Page 65 and 66: 3.2 Phase-shifting ESPI 63 ∞ ~ ~
Page 67 and 68: 3.2 Phase-shifting ESPI 65 ∞ N
Page 69 and 70: 3.2 Phase-shifting ESPI 67 The spec
Page 71 and 72: 3.2 Phase-shifting ESPI 69 − 0. 2
Page 73 and 74: 3.2 Phase-shifting ESPI 71 ν x 0 i
Page 75 and 76: 3.2 Phase-shifting ESPI 73 to think
Page 77 and 78: 3.3 Temporal phase shifting 75 Agai
Page 79 and 80: 3.3 Temporal phase shifting 77 addi
Page 81 and 82: 3.4 Spatial phase shifting 79 which
Page 83 and 84: 3.4 Spatial phase shifting 81 3.4.1
Page 85 and 86: 3.4 Spatial phase shifting 83 cross
Page 87 and 88: 3.4 Spatial phase shifting 85 Fig.
Page 89 and 90: 3.4 Spatial phase shifting 87 arran
Page 91 and 92: 3.4 Spatial phase shifting 89 infor
Page 93 and 94: 3.4 Spatial phase shifting 91 frequ
Page 95 and 96: 3.4 Spatial phase shifting 93 altho
Page 97 and 98: 3.4 Spatial phase shifting 95 error
Page 99: 3.4 Spatial phase shifting 97 Since
Page 102 and 103: 100 Quantification of displacement-
Page 112 and 113: 110
Page 114 and 115: 112 Comparison of noise in phase ma
Page 136 and 137: 134 Improvements on SPS intensity o
Page 138 and 139: 136 Improvements on SPS 0.14 σ d /
Page 140 and 141: 138 Improvements on SPS we are conc
Page 142 and 143: 140 Improvements on SPS 6.2 Modifie
Page 146 and 147: 144 Improvements on SPS Fig. 6.7 te
Page 148 and 149: 146 Improvements on SPS Finally, bo
Page 150 and 151: 148 Improvements on SPS To use the
Page 152 and 153: 150 Improvements on SPS The improve
Page 154 and 155: 152 Improvements on SPS On the whol
Page 156 and 157: 154 Improvements on SPS In classica
Page 158 and 159: 156 Improvements on SPS generally n
Page 162 and 163: 160 Improvements on SPS uncertain,
Page 164 and 165: 162 Improvements on SPS To obtain p
Page 166 and 167:
164 Improvements on SPS Fig. 6.22:
Page 168 and 169:
166 Improvements on SPS This proced
Page 170 and 171:
168 Improvements on SPS 6.7.2 Long-
Page 172 and 173:
170 Improvements on SPS Fig. 6.28:
Page 174 and 175:
172 Improvements on SPS the heater
Page 176 and 177:
174
Page 178 and 179:
176 Summary method to search for a
Page 180 and 181:
178
Page 182 and 183:
180 References [Bot97] [Bra87] [Bro
Page 184 and 185:
182 References [Ett97] [Fac93] [Far
Page 186 and 187:
184 References [Har94] [Her96] [Het
Page 188 and 189:
186 References [Kuj89] [Kuj91a] [Ku
Page 190 and 191:
188 References [McLa86] [Mer83] J.
Page 192 and 193:
190 References [Rav99] I. Raveh, E.
Page 194 and 195:
192 References [Sur98b] [Sur98c] [S
Page 196 and 197:
194
Page 198 and 199:
196 Appendix A: Counting events and
Page 200 and 201:
198 Appendix B: Real-time phase cal
Page 202 and 203:
200 Appendix C: Derivation of inten
Page 204 and 205:
I 1 a r g ( S ~ ( ) ) 202 Appendix
Page 206 and 207:
204 Appendix D: Alternative error-c
Page 208 and 209:
206
Page 210 and 211:
208
Page 212 and 213:
210 The author List of publications
Page 214:
212
show all

Application and Optimisation of the Spatial Phase Shifting ...

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?