Application and Optimisation of the Spatial Phase Shifting ...

a r g (
S
~
( ) )
201
Appendix D: Alternative error-compensating formulae
In Chapter 3.2.2, we have restricted ourselves to a maximum of four intensity samples in the phase
reconstruction formulae. If we do allow the inclusion of a fifth sample, we obtain one more degree of
freedom to customise the compensation of errors. In the context of spatial phase shifting, an interesting
solution has been presented in [Küch91, Küch97]. The derivation is based on the realisation that is it
possible to find three phase-shifting angles, or signal frequencies, for which the phase is determined
without error when five intensity samples are available. With one of them fixed at α=90°/sample, the
other two can be arranged symmetrically with respect to the nominal phase shift. In [Küch91], a formula
is described which works correctly at α=30, 90, and 150°/sample, and with little error in between. When
the intensity samples are weighted according to
ϕ
O
− I0 + 3( I1 − I3)
+ I4
mod 2π
= arctan
− I − I + 4I − I − I
0 1 2 3 4
, (D.1)
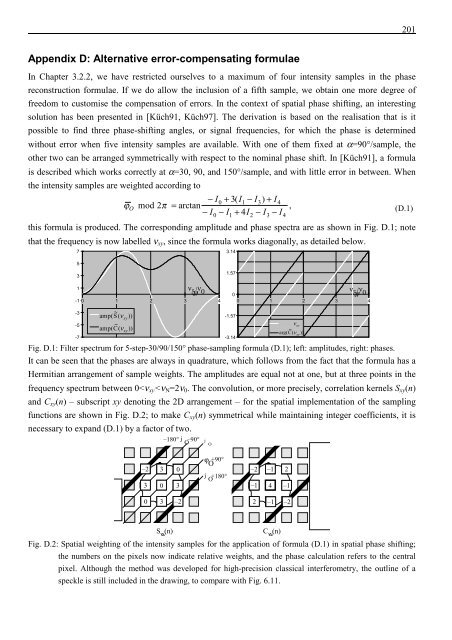
this formula is produced. The corresponding amplitude and phase spectra are as shown in Fig. D.1; note
that the frequency is now labelled ν xy , since the formula works diagonally, as detailed below.
7
3.14
5
3
1
-1 0 1 2 3 4
1.57
ν
0
ξψ
/ν 0
0 1 2 3 4
ν ξψ
/ν 0
-3.14
-3
-5
-7
amp( S
~ ( ν ))
xy
amp( C
~ ( ν ))
xy
-1.57
ν xy
arg( C
~ ( ν ))
Fig. D.1: Filter spectrum for 5-step-30/90/150° phase-sampling formula (D.1); left: amplitudes, right: phases.
It can be seen that the phases are always in quadrature, which follows from the fact that the formula has a
Hermitian arrangement of sample weights. The amplitudes are equal not at one, but at three points in the
frequency spectrum between 0