Application and Optimisation of the Spatial Phase Shifting ...

3.2 Phase-shifting ESPI 57
But remembering that we have initially been enforcing positive intensity values only to display them
conveniently on a screen, one might argue that there is no real need to do so. Therefore we have to settle
the question whether a kind of "signed" correlation fringes exists that circumvents the problems
associated with squaring or rectification. If we form fringes according to
I = I − I = 2 OR ( ϕ + ϕ − ϕ + α )
, , cos( ∆ ) cos( ) , (3.21)
n s f n i O O n
with the subscript s for "signed", all of the information is being preserved. Unfortunately, when we insert
these I n,s into a phase-shifting formula like (3.13), we cannot measure ∆ϕ: because of a = b = 0 , the
contributions from the first cosine are cancelled, and what we then measure by phase shifting is just the
speckle phase. This has been verified experimentally and demonstrates that really some information is
lacking from our reduced set of images I n,i and I 0,f .
Nonetheless, some specialised methods exist that can determine both ∆ϕ and ϕ O , correct for ϕ O and thus
generate acceptable sawtooth images from unfiltered correlation fringes. In [Kuj89] a so-called "speckle
phase correlation method" is derived for α=120° that indeed uses I {0,1,2},i and I * 0,f without filtering. The
same is done in [Moo94] for α=90° and I {0,1,2,3},i and I 0,f . However, none of these methods can find the
correct speckle phase without help: the equations involve an arccosine and a square root and have four
solutions, which again reflects the loss of information brought about by the rectification. This problem is
solved by initially generating a smoothed phase map ∆ϕ filt in the usual way (Fig. 3.4, right side), which
serves as a reference: that solution for ϕ O which brings ∆ϕ –ϕ O closest to ∆ϕ filt is selected as the correct
speckle phase and subtracted. In this way, the phase measurement from raw correlation fringes can be
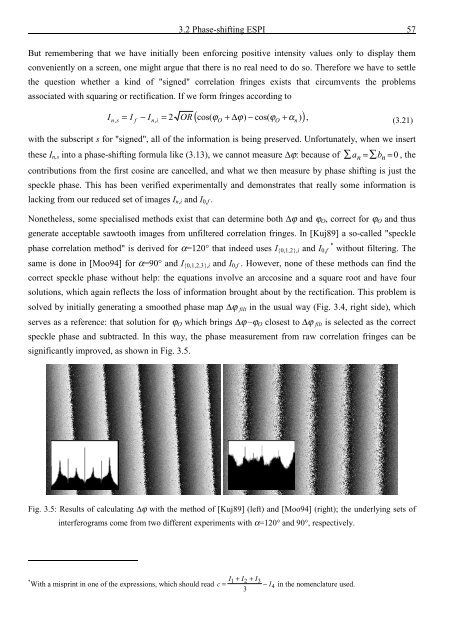
significantly improved, as shown in Fig. 3.5.
∑
n
∑
n
Fig. 3.5: Results of calculating ∆ϕ with the method of [Kuj89] (left) and [Moo94] (right); the underlying sets of
interferograms come from two different experiments with α=120° and 90°, respectively.
* I1 + I2 + I3
With a misprint in one of the expressions, which should read c =
− I4
in the nomenclature used.
3