Application and Optimisation of the Spatial Phase Shifting ...

124 Comparison of noise in phase maps from TPS and SPS
The sensitivity vector lies in the object's plane in horizontal direction; in this case, only x-displacements
can be measured. The object rotation generates 1.4 horizontal sawtooth fringes per wavelength of in-plane
displacement. Consequently, the conversion factor from phase to displacement is λ/509° or λ/(362 grey
levels), which is approximately halfway between the out-of-plane and the in-plane sensitivity that we have
previously been dealing with. (It would however be easy to increase this value: if both incidence angles
were 53°, as in 5.5.1, we would get 1.6 sawtooth fringes per wavelength of displacement.) The
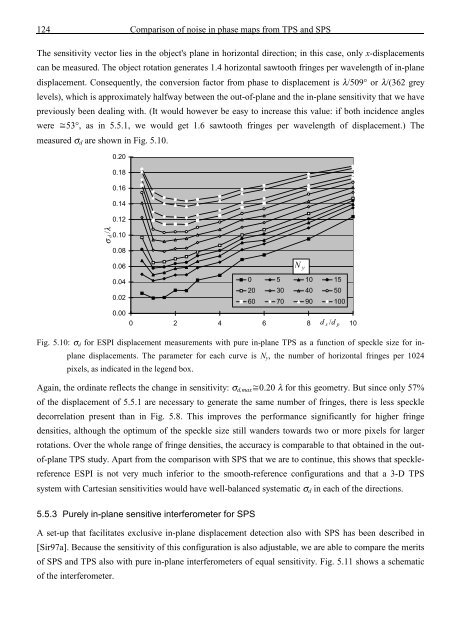
measured σ d are shown in Fig. 5.10.
σ d /λ
0.20
0.18
0.16
0.14
0.12
0.10
0.08
0.06
0.04
0.02
0.00
0 5 10 15
20 30 40 50
60 70 90 100
0 2 4 6 8 d s /d p 10
N y
Fig. 5.10: σ d for ESPI displacement measurements with pure in-plane TPS as a function of speckle size for inplane
displacements. The parameter for each curve is N y , the number of horizontal fringes per 1024
pixels, as indicated in the legend box.
Again, the ordinate reflects the change in sensitivity: σ d,max 0.20 λ for this geometry. But since only 57%
of the displacement of 5.5.1 are necessary to generate the same number of fringes, there is less speckle
decorrelation present than in Fig. 5.8. This improves the performance significantly for higher fringe
densities, although the optimum of the speckle size still wanders towards two or more pixels for larger
rotations. Over the whole range of fringe densities, the accuracy is comparable to that obtained in the outof-plane
TPS study. Apart from the comparison with SPS that we are to continue, this shows that specklereference
ESPI is not very much inferior to the smooth-reference configurations and that a 3-D TPS
system with Cartesian sensitivities would have well-balanced systematic σ d in each of the directions.
5.5.3 Purely in-plane sensitive interferometer for SPS
A set-up that facilitates exclusive in-plane displacement detection also with SPS has been described in
[Sir97a]. Because the sensitivity of this configuration is also adjustable, we are able to compare the merits
of SPS and TPS also with pure in-plane interferometers of equal sensitivity. Fig. 5.11 shows a schematic
of the interferometer.