Application and Optimisation of the Spatial Phase Shifting ...

6.1 Optimisation of experimental parameters 139
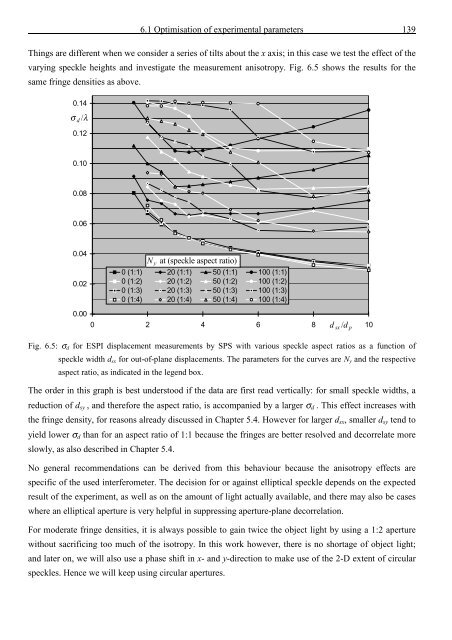
Things are different when we consider a series of tilts about the x axis; in this case we test the effect of the
varying speckle heights and investigate the measurement anisotropy. Fig. 6.5 shows the results for the
same fringe densities as above.
0.14
σ d /λ
0.12
0.10
0.08
0.06
0.04
0.02
0.00
N y at (speckle aspect ratio)
0 (1:1) 20 (1:1) 50 (1:1) 100 (1:1)
0 (1:2) 20 (1:2) 50 (1:2) 100 (1:2)
0 (1:3) 20 (1:3) 50 (1:3) 100 (1:3)
0 (1:4) 20 (1:4) 50 (1:4) 100 (1:4)
0 2 4 6 8 d sx /d p 10
Fig. 6.5: σ d for ESPI displacement measurements by SPS with various speckle aspect ratios as a function of
speckle width d sx for out-of-plane displacements. The parameters for the curves are N y and the respective
aspect ratio, as indicated in the legend box.
The order in this graph is best understood if the data are first read vertically: for small speckle widths, a
reduction of d sy , and therefore the aspect ratio, is accompanied by a larger σ d . This effect increases with
the fringe density, for reasons already discussed in Chapter 5.4. However for larger d sx , smaller d sy tend to
yield lower σ d than for an aspect ratio of 1:1 because the fringes are better resolved and decorrelate more
slowly, as also described in Chapter 5.4.
No general recommendations can be derived from this behaviour because the anisotropy effects are
specific of the used interferometer. The decision for or against elliptical speckle depends on the expected
result of the experiment, as well as on the amount of light actually available, and there may also be cases
where an elliptical aperture is very helpful in suppressing aperture-plane decorrelation.
For moderate fringe densities, it is always possible to gain twice the object light by using a 1:2 aperture
without sacrificing too much of the isotropy. In this work however, there is no shortage of object light;
and later on, we will also use a phase shift in x- and y-direction to make use of the 2-D extent of circular
speckles. Hence we will keep using circular apertures.