Application and Optimisation of the Spatial Phase Shifting ...

5.5 In-plane displacements 127
the first one on the abscissa. Nevertheless, the plots are scaled as in Fig. 5.10 to make the visual
comparison easier. Because we have a symmetrical 45° set-up also here, the conversion factors and σ d,max
are the same as in 5.5.2.
0.20
0.18
0.16
0.14
0.12
σ d /λ
0.10
0.08
0.06
0.04
0.02
0.00
0 5 10 15
20 30 40 50
60 70 90 100
0 2 4 6 8 d s /d p 10
N y
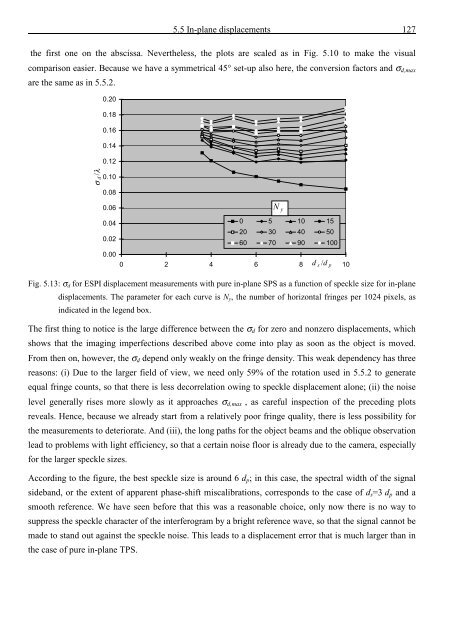
Fig. 5.13: σ d for ESPI displacement measurements with pure in-plane SPS as a function of speckle size for in-plane
displacements. The parameter for each curve is N y , the number of horizontal fringes per 1024 pixels, as
indicated in the legend box.
The first thing to notice is the large difference between the σ d for zero and nonzero displacements, which
shows that the imaging imperfections described above come into play as soon as the object is moved.
From then on, however, the σ d depend only weakly on the fringe density. This weak dependency has three
reasons: (i) Due to the larger field of view, we need only 59% of the rotation used in 5.5.2 to generate
equal fringe counts, so that there is less decorrelation owing to speckle displacement alone; (ii) the noise
level generally rises more slowly as it approaches σ d,max , as careful inspection of the preceding plots
reveals. Hence, because we already start from a relatively poor fringe quality, there is less possibility for
the measurements to deteriorate. And (iii), the long paths for the object beams and the oblique observation
lead to problems with light efficiency, so that a certain noise floor is already due to the camera, especially
for the larger speckle sizes.
According to the figure, the best speckle size is around 6 d p ; in this case, the spectral width of the signal
sideband, or the extent of apparent phase-shift miscalibrations, corresponds to the case of d s =3 d p and a
smooth reference. We have seen before that this was a reasonable choice, only now there is no way to
suppress the speckle character of the interferogram by a bright reference wave, so that the signal cannot be
made to stand out against the speckle noise. This leads to a displacement error that is much larger than in
the case of pure in-plane TPS.