Application and Optimisation of the Spatial Phase Shifting ...

70 Electronic or Digital Speckle Pattern Interferometry
bsc (ν x )
Re
bsc (ν x )
Re
bsc (ν x )
Re
~ C(
ν x )
~ C(
ν x )
~ C(
ν x )
~ S ( νx
)
Im
~ S ( νx
)
Im
~ S ( νx
)
Im
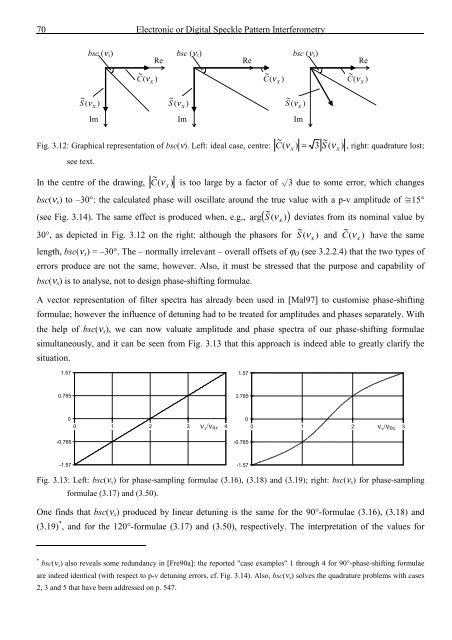
Fig. 3.12: Graphical representation of bsc(ν). Left: ideal case, centre: ~ C ( ν )
see text.
x
~
= 3 S ( ν ) , right: quadrature lost;
x
In the centre of the drawing, C
~ ( ν ) is too large by a factor of L3 due to some error, which changes
x
bsc(ν x ) to –30°: the calculated phase will oscillate around the true value with a p-v amplitude of 15°
(see Fig. 3.14). The same effect is produced when, e.g., arg ( S
~ ( ))
ν deviates from its nominal value by
30°, as depicted in Fig. 3.12 on the right: although the phasors for S
~ ( ν ) and C
~ ( ν ) have the same
length, bsc(ν x ) = –30°. The – normally irrelevant – overall offsets of ϕ O (see 3.2.2.4) that the two types of
errors produce are not the same, however. Also, it must be stressed that the purpose and capability of
bsc(ν x ) is to analyse, not to design phase-shifting formulae.
A vector representation of filter spectra has already been used in [Mal97] to customise phase-shifting
formulae; however the influence of detuning had to be treated for amplitudes and phases separately. With
the help of bsc(ν x ), we can now valuate amplitude and phase spectra of our phase-shifting formulae
simultaneously, and it can be seen from Fig. 3.13 that this approach is indeed able to greatly clarify the
situation.
x
x
x
1.57
1.57
0.785
0.785
0
0 1 2 3 4
0
0 1 2 ν x /ν 0x 3
ν x /ν 0x
-1.57
-0.785
-0.785
-1.57
Fig. 3.13: Left: bsc(ν x ) for phase-sampling formulae (3.16), (3.18) and (3.19); right: bsc(ν x ) for phase-sampling
formulae (3.17) and (3.50).
One finds that bsc(ν x ) produced by linear detuning is the same for the 90°-formulae (3.16), (3.18) and
(3.19) * , and for the 120°-formulae (3.17) and (3.50), respectively. The interpretation of the values for
* bsc(ν x ) also reveals some redundancy in [Fre90a]: the reported "case examples" 1 through 4 for 90°-phase-shifting formulae
are indeed identical (with respect to p-v detuning errors, cf. Fig. 3.14). Also, bsc(ν x ) solves the quadrature problems with cases
2, 3 and 5 that have been addressed on p. 547.