- Page 1:
Observatoire de Paris, Universités
- Page 4 and 5:
4 TABLE DES MATIÈRES 2.6.2 Équati
- Page 6 and 7:
6 TABLE DES MATIÈRES 6.3.3 Jauge d
- Page 8 and 9:
8 TABLE DES MATIÈRES Bibliographie
- Page 10 and 11:
10 Introduction purement newtonienn
- Page 12 and 13:
12 Introduction
- Page 14 and 15:
14 Cadre géométrique Fig. 2.1 - V
- Page 16 and 17:
16 Cadre géométrique égard n’e
- Page 18 and 19:
18 Cadre géométrique Fig. 2.4 - E
- Page 20 and 21:
20 Cadre géométrique x e x z e z
- Page 22 and 23:
22 Cadre géométrique où v est le
- Page 24 and 25:
24 Cadre géométrique 1. Comme dis
- Page 26 and 27:
26 Cadre géométrique En reportant
- Page 28 and 29:
28 Cadre géométrique 2.3.4 Genre
- Page 30 and 31:
30 Cadre géométrique la métrique
- Page 32 and 33:
32 Cadre géométrique Fig. 2.9 - C
- Page 34 and 35:
34 Cadre géométrique Fig. 2.11 -
- Page 36 and 37:
36 Cadre géométrique simple que s
- Page 38 and 39:
38 Cadre géométrique Fig. 2.12 -
- Page 40 and 41:
40 Cadre géométrique Fig. 2.14 -
- Page 42 and 43:
42 Cadre géométrique Fig. 2.16 -
- Page 44 and 45:
44 Cadre géométrique Fig. 2.18 -
- Page 46 and 47:
46 Cadre géométrique 2.6 Principe
- Page 48 and 49:
48 Cadre géométrique En multiplia
- Page 50 and 51:
50 Cadre géométrique En reportant
- Page 52 and 53:
52 Cadre géométrique
- Page 54 and 55:
54 Champ gravitationnel à symétri
- Page 56 and 57:
56 Champ gravitationnel à symétri
- Page 58 and 59:
58 Champ gravitationnel à symétri
- Page 60 and 61:
60 Champ gravitationnel à symétri
- Page 62 and 63:
62 Champ gravitationnel à symétri
- Page 64 and 65:
64 Champ gravitationnel à symétri
- Page 66 and 67:
66 Champ gravitationnel à symétri
- Page 68 and 69:
68 Champ gravitationnel à symétri
- Page 70 and 71:
70 Champ gravitationnel à symétri
- Page 72 and 73:
72 Champ gravitationnel à symétri
- Page 74 and 75:
74 Champ gravitationnel à symétri
- Page 76 and 77: 76 Champ gravitationnel à symétri
- Page 78 and 79: 78 Champ gravitationnel à symétri
- Page 80 and 81: 80 Champ gravitationnel à symétri
- Page 82 and 83: 82 Champ gravitationnel à symétri
- Page 84 and 85: 84 Champ gravitationnel à symétri
- Page 86 and 87: 86 Champ gravitationnel à symétri
- Page 88 and 89: 88 Champ gravitationnel à symétri
- Page 90 and 91: 90 Champ gravitationnel à symétri
- Page 92 and 93: 92 Champ gravitationnel à symétri
- Page 94 and 95: 94 Équation d’Einstein 4.2 Déri
- Page 96 and 97: 96 Équation d’Einstein 4.2.2 Dé
- Page 98 and 99: 98 Équation d’Einstein Remarque
- Page 100 and 101: 100 Équation d’Einstein formes l
- Page 102 and 103: 102 Équation d’Einstein géodés
- Page 104 and 105: 104 Équation d’Einstein On dit a
- Page 106 and 107: 106 Équation d’Einstein Si on ut
- Page 108 and 109: 108 Équation d’Einstein Fig. 4.2
- Page 110 and 111: 110 Équation d’Einstein 4.3.2 Pr
- Page 112 and 113: 112 Équation d’Einstein • La c
- Page 114 and 115: 114 Équation d’Einstein Γ suppl
- Page 116 and 117: 116 Équation d’Einstein 4.6 Solu
- Page 118 and 119: 118 Équation d’Einstein 4.6.2 So
- Page 120 and 121: 120 Équation d’Einstein les comp
- Page 122 and 123: 122 Équation d’Einstein
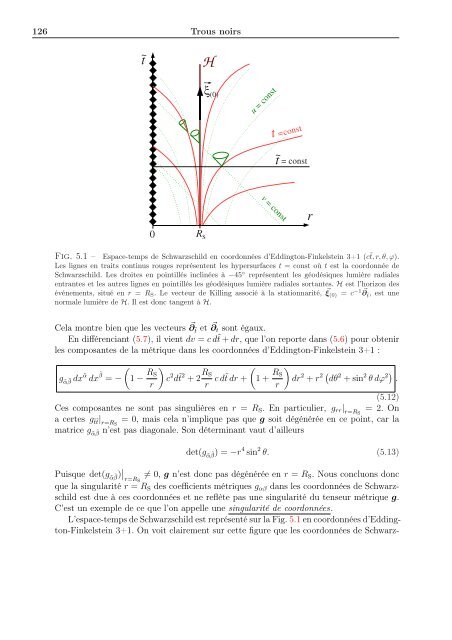
- Page 124 and 125: 124 Trous noirs de la gravitation,
- Page 128 and 129: 128 Trous noirs 5.3.1 Définition D
- Page 130 and 131: 130 Trous noirs Fig. 5.2 - Image d
- Page 132 and 133: 132 Trous noirs Au vu de (5.24), on
- Page 134 and 135: 134 Trous noirs horizon ergosphère
- Page 136 and 137: 136 Trous noirs où nous avons intr
- Page 138 and 139: 138 Trous noirs l’on compare avec
- Page 140 and 141: 140 Trous noirs Fig. 5.6 - Processu
- Page 142 and 143: 142 Trous noirs
- Page 144 and 145: 144 Ondes gravitationnelles Fig. 6.
- Page 146 and 147: 146 Ondes gravitationnelles Auparav
- Page 148 and 149: 148 Ondes gravitationnelles où l
- Page 150 and 151: 150 Ondes gravitationnelles On peut
- Page 152 and 153: 152 Ondes gravitationnelles Chercho
- Page 154 and 155: 154 Ondes gravitationnelles coordon
- Page 156 and 157: 156 Ondes gravitationnelles Fig. 6.
- Page 158 and 159: 158 Ondes gravitationnelles Remarqu
- Page 160 and 161: 160 Ondes gravitationnelles Ξ ≪
- Page 162 and 163: 162 Ondes gravitationnelles On reco
- Page 164 and 165: 164 Ondes gravitationnelles Si M es
- Page 166 and 167: 166 Ondes gravitationnelles Fig. 6.
- Page 168 and 169: 168 Solutions cosmologiques 7.2 Esp
- Page 170 and 171: 170 Solutions cosmologiques Elles s
- Page 172 and 173: 172 Solutions cosmologiques Fig. 7.
- Page 174 and 175: 174 Solutions cosmologiques Examino
- Page 176 and 177:
176 Solutions cosmologiques Fig. 7.
- Page 178 and 179:
178 Solutions cosmologiques où les
- Page 180 and 181:
180 Solutions cosmologiques π/2. O
- Page 182 and 183:
182 Solutions cosmologiques Fig. 7.
- Page 184 and 185:
184 Solutions cosmologiques et 2(x
- Page 186 and 187:
186 Solutions cosmologiques Exprimo
- Page 188 and 189:
188 Solutions cosmologiques Fig. 7.
- Page 190 and 191:
190 Solutions cosmologiques En comp
- Page 192 and 193:
192 Solutions cosmologiques fonctio
- Page 194 and 195:
194 Solutions cosmologiques courbes
- Page 196 and 197:
196 Solutions cosmologiques droite
- Page 198 and 199:
198 Solutions cosmologiques ä 1 +
- Page 200 and 201:
200 Solutions cosmologiques où a0,
- Page 202 and 203:
202 Solutions cosmologiques
- Page 204 and 205:
204 Relativité et GPS Fig. A.1 - C
- Page 206 and 207:
206 Relativité et GPS donné par g
- Page 208 and 209:
208 Relativité et GPS où la const
- Page 210 and 211:
210 Relativité et GPS Il vient alo
- Page 212 and 213:
212 Relativité et GPS
- Page 214 and 215:
214 Problèmes tourne autour de l
- Page 216 and 217:
216 Problèmes 10 Effectuer les lim
- Page 218 and 219:
218 Problèmes 8 En déduire que, p
- Page 220 and 221:
220 Problèmes 2.1 En raisonnant su
- Page 222 and 223:
222 Problèmes 3.4 Que vaut la coor
- Page 224 and 225:
224 Problèmes 10 Calculer δτ :=
- Page 226 and 227:
226 Problèmes En supposant un flui
- Page 228 and 229:
228 Problèmes 2 Montrer que les ve
- Page 230 and 231:
230 Problèmes 4 Montrer que la con
- Page 232 and 233:
232 Problèmes surface par unité d
- Page 234 and 235:
234 Problèmes 5 Montrer que u r
- Page 236 and 237:
236 Problèmes vers Fig. B.1 - Traj
- Page 238 and 239:
238 Problèmes 1. K est symétrique
- Page 240 and 241:
240 Problèmes les coordonnées de
- Page 242 and 243:
242 Problèmes dont les composantes
- Page 244 and 245:
244 Problèmes
- Page 246 and 247:
246 Solutions des problèmes + 1 +
- Page 248 and 249:
248 Solutions des problèmes 8 L’
- Page 250 and 251:
250 Solutions des problèmes Par ai
- Page 252 and 253:
252 Solutions des problèmes Fig. C
- Page 254 and 255:
254 Solutions des problèmes 7 Les
- Page 256 and 257:
256 Solutions des problèmes Remarq
- Page 258 and 259:
258 Solutions des problèmes a c t
- Page 260 and 261:
260 Solutions des problèmes ∂0 e
- Page 262 and 263:
262 Solutions des problèmes a c t
- Page 264 and 265:
264 Solutions des problèmes a cτ
- Page 266 and 267:
266 Solutions des problèmes 4 Si l
- Page 268 and 269:
268 Solutions des problèmes (obser
- Page 270 and 271:
270 Solutions des problèmes Soit v
- Page 272 and 273:
272 Solutions des problèmes d’o
- Page 274 and 275:
274 Solutions des problèmes p / (
- Page 276 and 277:
276 Solutions des problèmes Ξmax
- Page 278 and 279:
278 Solutions des problèmes De mê
- Page 280 and 281:
280 Solutions des problèmes On rec
- Page 282 and 283:
282 Solutions des problèmes 6 Par
- Page 284 and 285:
284 Solutions des problèmes On en
- Page 286 and 287:
286 Solutions des problèmes On a,
- Page 288 and 289:
288 Solutions des problèmes Comme
- Page 290 and 291:
290 Solutions des problèmes La sol
- Page 292 and 293:
292 Solutions des problèmes est un
- Page 294 and 295:
294 Solutions des problèmes Fig. C
- Page 296 and 297:
296 Solutions des problèmes Fig. C
- Page 298 and 299:
298 Solutions des problèmes C.13 T
- Page 300 and 301:
300 Solutions des problèmes + 2mr
- Page 302 and 303:
302 Solutions des problèmes C.14 G
- Page 304 and 305:
304 Solutions des problèmes H éta
- Page 306 and 307:
306 Solutions des problèmes où l
- Page 308 and 309:
308 Solutions des problèmes 12 On
- Page 310 and 311:
310 Solutions des problèmes
- Page 312 and 313:
312 Codes Sage n = 2 ; var(’th’
- Page 314 and 315:
314 Codes Sage Le tenseur de Ricci
- Page 316 and 317:
316 BIBLIOGRAPHIE [16] P. Peter & J
- Page 318 and 319:
318 BIBLIOGRAPHIE [42] D. Bini, R.T
- Page 320 and 321:
Index (GCRS), 206 (TAI), 208 (TT),
- Page 322 and 323:
322 INDEX force de Poynting-Roberts
- Page 324:
324 INDEX rayon gravitationnel, 56