Microseismic Monitoring and Geomechanical Modelling of CO2 - bris

5.2. EFFECTIVE STRESS AND STRESS PATH PARAMETERS
30
25
Initial
Post injection
τ
20
15
Yield envelope
10
5
σ'1 σ'3
0
0 10 20 30 40 50
σ'n
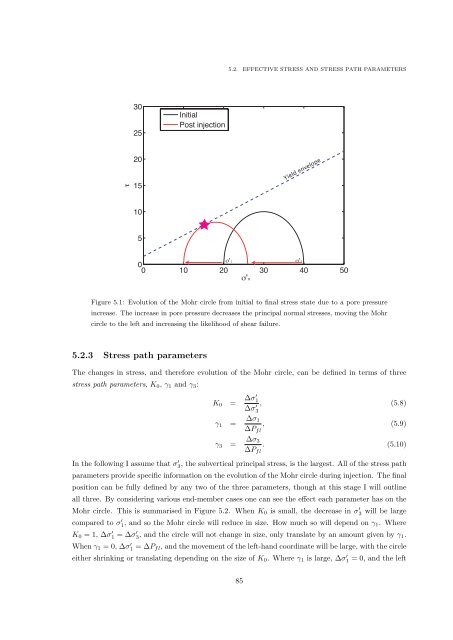
Figure 5.1: Evolution of the Mohr circle from initial to final stress state due to a pore pressure
increase. The increase in pore pressure decreases the principal normal stresses, moving the Mohr
circle to the left and increasing the likelihood of shear failure.
5.2.3 Stress path parameters
The changes in stress, and therefore evolution of the Mohr circle, can be defined in terms of three
stress path parameters, K 0 , γ 1 and γ 3 :
K 0 = ∆σ′ 1
∆σ ′ , (5.8)
3
γ 1 = ∆σ 1
∆P fl
, (5.9)
γ 3 = ∆σ 3
∆P fl
. (5.10)
In the following I assume that σ ′ 3, the subvertical principal stress, is the largest. All of the stress path
parameters provide specific information on the evolution of the Mohr circle during injection. The final
position can be fully defined by any two of the three parameters, though at this stage I will outline
all three. By considering various end-member cases one can see the effect each parameter has on the
Mohr circle. This is summarised in Figure 5.2. When K 0 is small, the decrease in σ ′ 3 will be large
compared to σ ′ 1, and so the Mohr circle will reduce in size. How much so will depend on γ 1 . Where
K 0 = 1, ∆σ ′ 1 = ∆σ ′ 3, and the circle will not change in size, only translate by an amount given by γ 1 .
When γ 1 = 0, ∆σ ′ 1 = ∆P fl , and the movement of the left-hand coordinate will be large, with the circle
either shrinking or translating depending on the size of K 0 . Where γ 1 is large, ∆σ ′ 1 = 0, and the left
85