Microseismic Monitoring and Geomechanical Modelling of CO2 - bris

3.2. INVERSION METHOD
180
160
140
Crack normal compliance (×10 −11 Pa −1 )
1.4
1.2
1
P i
120
100
80
0.8
0.6
60
40
20
0.4
0.2
0
−6 −5 −4 −3 −2 −1
log 10
(P ep
)
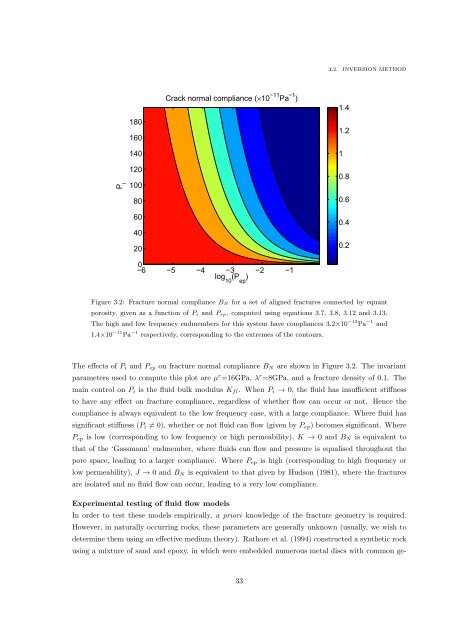
Figure 3.2: Fracture normal compliance B N for a set of aligned fractures connected by equant
porosity, given as a function of P i and P ep , computed using equations 3.7, 3.8, 3.12 and 3.13.
The high and low frequency endmembers for this system have compliances 3.2×10 −13 Pa −1 and
1.4×10 −11 Pa −1 respectively, corresponding to the extremes of the contours.
The effects of P i and P ep on fracture normal compliance B N are shown in Figure 3.2. The invariant
parameters used to compute this plot are µ r =16GPa, λ r =8GPa, and a fracture density of 0.1. The
main control on P i is the fluid bulk modulus K fl . When P i → 0, the fluid has insufficient stiffness
to have any effect on fracture compliance, regardless of whether flow can occur or not. Hence the
compliance is always equivalent to the low frequency case, with a large compliance. Where fluid has
significant stiffness (P i ≠ 0), whether or not fluid can flow (given by P ep ) becomes significant. Where
P ep is low (corresponding to low frequency or high permeability), K → 0 and B N is equivalent to
that of the ‘Gassmann’ endmember, where fluids can flow and pressure is equalised throughout the
pore space, leading to a larger compliance. Where P ep is high (corresponding to high frequency or
low permeability), J → 0 and B N is equivalent to that given by Hudson (1981), where the fractures
are isolated and no fluid flow can occur, leading to a very low compliance.
Experimental testing of fluid flow models
In order to test these models empirically, a priori knowledge of the fracture geometry is required.
However, in naturally occurring rocks, these parameters are generally unknown (usually, we wish to
determine them using an effective medium theory). Rathore et al. (1994) constructed a synthetic rock
using a mixture of sand and epoxy, in which were embedded numerous metal discs with common ge-
33