Microseismic Monitoring and Geomechanical Modelling of CO2 - bris

More documents

Recommendations

Info

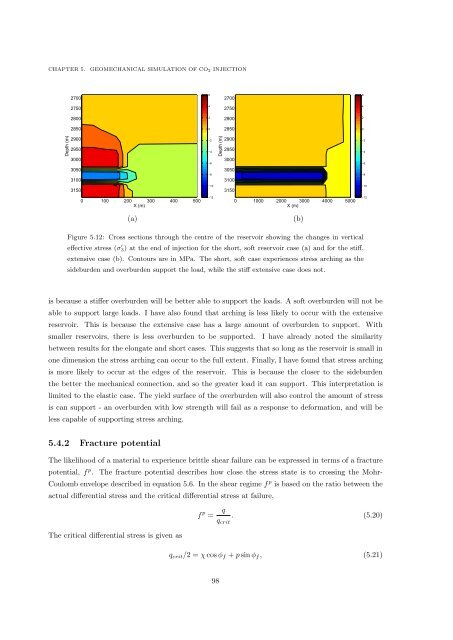
CHAPTER 5. GEOMECHANICAL SIMULATION OF CO 2 INJECTION 2700 6 2700 6 2750 4 2750 4 2800 2 2800 2 2850 0 2850 0 Depth (m) 2900 2950 3000 −2 −4 −6 Depth (m) 2900 2950 3000 −2 −4 −6 3050 3100 −8 3050 3100 −8 3150 −10 3150 −10 0 100 200 300 400 500 X (m) −12 0 1000 2000 3000 4000 5000 X (m) −12 (a) (b) Figure 5.12: Cross sections through the centre of the reservoir showing the changes in vertical effective stress (σ ′ 3) at the end of injection for the short, soft reservoir case (a) and for the stiff, extensive case (b). Contours are in MPa. The short, soft case experiences stress arching as the sideburden and overburden support the load, while the stiff extensive case does not. is because a stiffer overburden will be better able to support the loads. A soft overburden will not be able to support large loads. I have also found that arching is less likely to occur with the extensive reservoir. This is because the extensive case has a large amount of overburden to support. With smaller reservoirs, there is less overburden to be supported. I have already noted the similarity between results for the elongate and short cases. This suggests that so long as the reservoir is small in one dimension the stress arching can occur to the full extent. Finally, I have found that stress arching is more likely to occur at the edges of the reservoir. This is because the closer to the sideburden the better the mechanical connection, and so the greater load it can support. This interpretation is limited to the elastic case. The yield surface of the overburden will also control the amount of stress is can support - an overburden with low strength will fail as a response to deformation, and will be less capable of supporting stress arching. 5.4.2 Fracture potential The likelihood of a material to experience brittle shear failure can be expressed in terms of a fracture potential, f p . The fracture potential describes how close the stress state is to crossing the Mohr- Coulomb envelope described in equation 5.6. In the shear regime f p is based on the ratio between the actual differential stress and the critical differential stress at failure, The critical differential stress is given as f p = q q crit . (5.20) q crit /2 = χ cos ϕ f + p sin ϕ f , (5.21) 98
5.4. RESULTS 1z:100x:100y 1z:100x:5y 1z:5x:5y 10 10 10 5 5 5 Soft ∆ f p 0 −5 ∆ f p 0 −5 ∆ f p 0 −5 −10 −10 −10 −15 1 2 3 4 5 6 Timestep −15 1 2 3 4 5 6 Timestep −15 1 2 3 4 5 6 Timestep 10 10 10 5 5 5 Medium ∆ f p 0 −5 ∆ f p 0 −5 ∆ f p 0 −5 −10 −10 −10 −15 1 2 3 4 5 6 Timestep −15 1 2 3 4 5 6 Timestep −15 1 2 3 4 5 6 Timestep 10 10 10 5 5 5 Stiff ∆ f p 0 −5 ∆ f p 0 −5 ∆ f p 0 −5 −10 −10 −10 −15 1 2 3 4 5 6 Timestep −15 1 1.5 2 2.5 3 3.5 4 4.5 5 Timestep −15 1 2 3 4 5 6 Timestep Figure 5.13: Percentage change in fracture potential during injection into the simple reservoirs. I plot the fracture potentials for all the cells examined - in the centre of the reservoir (black), at the edge of the reservoir (red), in the corner of the reservoir (blue), in the overburden (green) and in the sideburden (magenta). Increases in fracture potential are seen for the smaller reservoirs (1z:100x:5y and 1z:5x:5y). The extensive reservoir (1z:100x:100y) models do not see increases in fracture potential either in the reservoir or the overburden. making the fracture potential f p = q 2(χ cos ϕ f + p sin ϕ f ) . (5.22) In Figure 5.13 I plot the percentage change in fracture potential through time for all of the simple reservoirs. To compute the results I use generic values for χ and ϕ f , with χ=5MPa and ϕ f =40 ◦ (m=0.84). Cases where f p increase represent cases where we might expect failure. I note that for the extensive reservoirs the values of f p do not change in the overburden, because the reservoirs are too extensive for the overburden to be supported, and so stress is not transferred. The values of f p in the reservoir decrease because, with a low value of K 0 , the Mohr circles will shrink, meaning that differential stresses are lower. Therefore I infer that the risk of shear failure for these cases is not only not increasing, but is in fact reducing. In contrast, the smaller reservoirs show f p values increasing during injection. For the softer reservoir it is in the overburden that the fracture potential is increasing, because stresses are transferred to the overburden, increasing the vertical stress while the horizontal stress is essentially unchanged, leading to a higher differential stress. For the stiffer reservoir it is inside the reservoir that f p increases 99
Page 1:
Microseismic Monitoring and Geomech
Page 5 and 6:
Abstract Capture of CO 2 produced a
Page 7 and 8:
Author’s Declaration I declare th
Page 9 and 10:
Acknowledgments There are many thin
Page 11 and 12:
Table of Contents Abstract Author
Page 13 and 14:
TABLE OF CONTENTS 5.4 Results . . .
Page 15 and 16:
Preface ‘Research is not an end i
Page 17 and 18:
6. D. Angus, J-M. Kendall, J.P. Ver
Page 19 and 20:
1 Introduction A technology push ap
Page 21 and 22:
1.2. CCS OVERVIEW Figure 1.2: CCS s
Page 23 and 24:
1.3. THESIS OVERVIEW for CO 2 to be
Page 25 and 26:
1.3. THESIS OVERVIEW as microseismi
Page 27 and 28:
2 The Weyburn CO 2 injection projec
Page 29 and 30:
2.2. WEYBURN GEOLOGICAL SETTING Fig
Page 31 and 32:
2.2. WEYBURN GEOLOGICAL SETTING N F
Page 33 and 34:
2.4. EVENT TIMING AND LOCATIONS 500
Page 35 and 36:
2.4. EVENT TIMING AND LOCATIONS 500
Page 37 and 38:
2.4. EVENT TIMING AND LOCATIONS Nor
Page 39 and 40:
2.4. EVENT TIMING AND LOCATIONS Fig
Page 41 and 42:
2.5. DISCUSSION 500 1000 1100 North
Page 43 and 44:
2.6. SUMMARY 2.6 Summary • CO 2 s
Page 45 and 46:
3 Inverting shear-wave splitting me
Page 47 and 48:
3.2. INVERSION METHOD the additiona
Page 49 and 50:
3.2. INVERSION METHOD 1. P-wave inc
Page 51 and 52:
3.2. INVERSION METHOD 180 160 140 C
Page 53 and 54:
3.2. INVERSION METHOD 2800 2800 260
Page 55 and 56:
3.2. INVERSION METHOD Loop over γ,
Page 57 and 58:
20 10 5 5 1 20 30 40 80 100 60 40 1
Page 59 and 60:
3.4. SWS MEASUREMENTS AT WEYBURN th
Page 61 and 62:
3.4. SWS MEASUREMENTS AT WEYBURN ei
Page 63 and 64:
3.4. SWS MEASUREMENTS AT WEYBURN ξ
Page 65 and 66: 3.4. SWS MEASUREMENTS AT WEYBURN da
Page 67 and 68: 4 2 2 3.4. SWS MEASUREMENTS AT WEYB
Page 69 and 70: 1 1 1 1 1 1 1 1 1 1 3.5. DISCUSSION
Page 71 and 72: 3.6. SUMMARY 3.6 Summary • I have
Page 73 and 74: 4 A comparison of microseismic moni
Page 75 and 76: 4.2. EVENT LOCATIONS 2400 Velocity
Page 77 and 78: 4.2. EVENT LOCATIONS 200 150 Northi
Page 79 and 80: 4.3. EVENT MAGNITUDES Pressure (MPa
Page 81 and 82: 4.3. EVENT MAGNITUDES 160 140 120 N
Page 83 and 84: 4.4. SHEAR WAVE SPLITTING 50 −3 E
Page 85 and 86: 4.5. INITIAL S-WAVE POLARISATION In
Page 87 and 88: 4.5. INITIAL S-WAVE POLARISATION 6
Page 89 and 90: 4.5. INITIAL S-WAVE POLARISATION of
Page 91 and 92: 4.6. INTERPRETATION OF SHEAR WAVE S
Page 93 and 94: 1 1 5 5 30 4.6. INTERPRETATION OF S
Page 95 and 96: 80 4.6. INTERPRETATION OF SHEAR WAV
Page 97 and 98: 2 3 3.5 4 5 2 1.8 1.4 4 4.6. INTERP
Page 99 and 100: 4.7. DISCUSSION 4.7 Discussion The
Page 101 and 102: pressure, P fl σ ′ ij = σ ij
Page 103 and 104: 5.2. EFFECTIVE STRESS AND STRESS PA
Page 105 and 106: 5.3. NUMERICAL MODELLING 5.3.1 Flui
Page 107 and 108: 5.3. NUMERICAL MODELLING MORE FLUID
Page 109 and 110: 5.3. NUMERICAL MODELLING (a) (b) Fi
Page 111 and 112: 5.4. RESULTS 0 500 1000 Depth (m) 1
Page 113 and 114: 5.4. RESULTS 1 0.9 0.8 Soft Med Sti
Page 115: 5.4. RESULTS Overburden Extension i
Page 119 and 120: 5.5. SURFACE UPLIFT 1 0.9 0.8 Soft
Page 121 and 122: 5.5. SURFACE UPLIFT Figure 5.17: Ma
Page 123 and 124: 6 Generating anisotropic seismic mo
Page 125 and 126: 6.2. STRESS-SENSITIVE ROCK PHYSICS
Page 127 and 128: 6.3. A MICRO-STRUCTURAL MODEL FOR N
Page 145 and 146: 6.4. CALIBRATION WITH LITERATURE DA
Page 147 and 148: 6.4. CALIBRATION WITH LITERATURE DA
Page 149 and 150: 6.5. COMPARISON OF ROCK PHYSICS MOD
Page 151 and 152: 6.5. COMPARISON OF ROCK PHYSICS MOD
Page 153 and 154: 7 Forward modelling of seismic prop
Page 155 and 156: 7.2. SEISMODEL c⃝ WORKFLOW time s
Page 157 and 158: 7.3. RESULTS FROM SIMPLE GEOMECHANI
Page 163 and 164: 7.4. SUMMARY 7.4 Summary • I have
Page 165 and 166: 8 Linking geomechanical modelling a
Page 167 and 168:
8.2. MODEL DESCRIPTION Layer Thickn
Page 169 and 170:
8.2. MODEL DESCRIPTION Unit E (GPa)
Page 171 and 172:
8.3. RESULTS Marl Vugg 0.8 0.8 Norm
Page 173 and 174:
8.3. RESULTS 15 10 Injector Produce
Page 175 and 176:
8.3. RESULTS 2000 15 2000 15 1500 1
Page 177 and 178:
8.4. A SOFTER RESERVOIR 8.4 A softe
Page 179 and 180:
8.4. A SOFTER RESERVOIR 2000 15 200
Page 181 and 182:
8.4. A SOFTER RESERVOIR 2000 Max SW
Page 183 and 184:
8.5. DISCUSSION pore-pressure being
Page 185 and 186:
8.6. SUMMARY 8.6 Summary • I appl
Page 187 and 188:
9 Conclusions Geological storage wi
Page 189 and 190:
calibrate. This model has been cali
Page 191 and 192:
9.1. NOVEL CONTRIBUTIONS techniques
Page 193 and 194:
9.2. FUTURE WORK Finally, the compa
Page 195 and 196:
Bibliography Abt, D. L., Fischer, K
Page 197 and 198:
BIBLIOGRAPHY Gassmann, F., 1951. Ub
Page 199 and 200:
BIBLIOGRAPHY Kendall, J.-M., Pilido
Page 201 and 202:
BIBLIOGRAPHY Sayers, C. M., 2002. S
Page 203 and 204:
BIBLIOGRAPHY White, D., 2009. Monit
Page 205 and 206:
A List of Symbols The table below l
Page 207 and 208:
B In Support of Carbon Capture and
Page 209 and 210:
Both China and India are aggressive
Page 211 and 212:
Utsira rock properties vary signifi
show all

Microseismic Monitoring and Geomechanical Modelling of CO2 - bris

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?